Vytvorenie ekonometrického modelu
Cieľom tejto fázy modelovania je zvoliť, čo budeme pomocou dát vysvetľovať, ktoré faktory môžu daný jav ovplyvňovať a aký tvar vzťahu medzi premennými predpokladáme. Našou úlohou je tento vzťah zapísať do matematickej podoby tak, aby ho bolo možné neskôr kvantifikovať a overovať pomocou dát.
Ekonometrický model
Ekonometrický model vyjadruje vzťah medzi závislou (vysvetľovanou) premennou a jednou alebo viacerými nezávislými (vysvetľujúcimi) premennými. Okrem toho obsahuje aj náhodnú zložku, ktorá zachytáva vplyvy, ktoré nie sú v modeli explicitne zahrnuté.
Čo všetko zahŕňa/nezahŕňa vytvorenie modelu
- ✔ voľbu závislej a vysvetľujúcich premenných
- ✔ zápis tvaru modelu (rovnice)
- ✔ vysvetlenie významu parametrov a náhodnej zložky
- ✖ odhad parametrov
- ✖ testovanie predpokladov modelu
Lineárna regresia
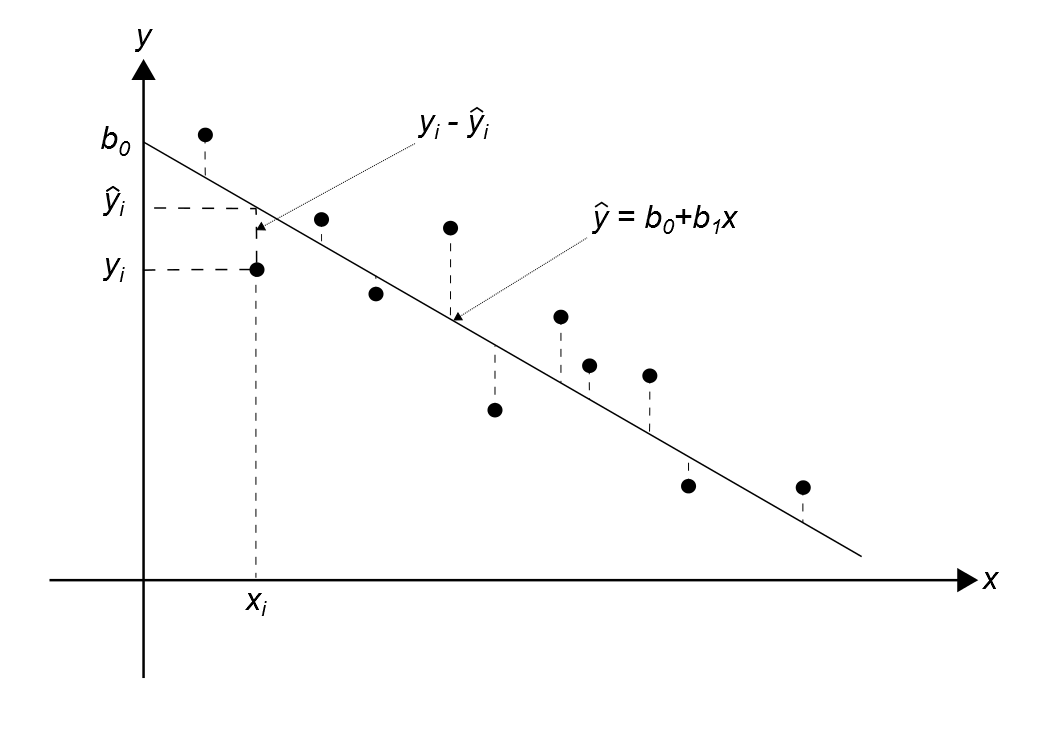
Lineárna regresia je metóda na popis vzťahu medzi závislou (vysvetľovanou) premennou y a nezávislou (vysvetľujúcou) premennou x. V jednoduchom prípade (na obrázku) hľadáme priamku ŷ = b0 + b1x, ktorá čo najlepšie vystihuje trend v dátach.
Pre každý bod platí, že rozdiel medzi skutočnou hodnotou a hodnotou na priamke sa nazýva reziduum: ei = yi − ŷi. Parametre b0 a b1 odhadneme metódou najmenších štvorcov (OLS) tak, aby bol súčet štvorcov rezíduí minimálny.
Vo všeobecnosti môžeme model zapísať tak, že predpovedaná hodnota závislej (vysvetľovanej) premennej je ŷi = f(xi, b1, …, bk), kde f je funkcia lineárna v parametroch b (napr. lineárna kombinácia vysvetľujúcich premenných). Parametre b1, …, bk sa odhadnú tak, aby bol minimálny súčet štvorcov rezíduí:

Ako prvý a najjednoduchší prípad si v ďalšej časti ukážeme lineárny jednorovnicový model, ktorý nám umožní ilustrovať vzťah medzi závislou a vysvetľujúcimi premennými v najjednoduchšej forme.
Jednorovnicový model
Jednorovnicový (lineárny regresný) model popisuje vzťah medzi závislou (vysvetľovanou) premennou y a jednou alebo viacerými nezávislými (vysvetľujúcimi) premennými x. Pre pozorovania t = 1, 2, …, n ho zapisujeme:
yt = β0 + β1xt1 + … + βkxtk + ut
- yt – hodnota závislej (vysvetľovanej) premennej v čase/pozorovaní t
- xt1, …, xtk – hodnoty nezávislých (vysvetľujúcich) premenných
- β0, β1, …, βk – neznáme parametre modelu, ktoré odhadujeme z dát
- ut – náhodná zložka (chyba), ktorá zahŕňa vplyvy, ktoré nie sú v modeli explicitne zachytené
Model je možné zapísať aj v maticovom tvare, ktorý je praktický pri práci s viacerými premennými:
y = Xβ + u
- y – vektor pozorovaní závislej premennej (rozmer n × 1)
- X – matica nezávislých premenných (rozmer n × (k+1)), pričom prvý stĺpec býva tvorený jednotkami (pre β0)
- β – vektor parametrov (rozmer (k+1) × 1)
- u – vektor náhodných chýb (rozmer n × 1)
Po odhade parametrov dostaneme β̂ a vypočítané (predpovedané) hodnoty závislej premennej:
ŷ = Xβ̂.
Rozdiel medzi skutočnými a predpovedanými hodnotami nazývame reziduá:
e = y − ŷ.
Marček, D., Marček, M., Pančíková, L.: Ekonometria a soft computing. Žilina: EDIS, 2008. ISBN 978-80-8070-746-0
Gujarati, D. N., Porter, D. C.: Basic Econometrics. McGraw-Hill, 2009.
EOLSS: Econometric Methods / Applied Econometric Analysis.
https://www.eolss.net/sample-chapters/c02/e6-154-06.pdf
Lineární regrese tak nebo jinak [4. 6. 2015]
Metoda nejmenších čtverců [4. 6. 2015]
