Prognózovanie s využitím spektrálnej analýzy
Existuje mnoho publikácií a vedeckých článkov, ktoré dokazujú dôležitú úlohu spektrálnej analýzy pri dekompozícii časových radov, a to s cieľom určiť ich primárne cykly, dlhodobé trendy, sezónne vplyvy a pod. Autori však boli a stále sú zdržanliví ohľadom využitia spektrálnej analýzy priamo pre účely prognózovania.
Spektrálnu analýzu pre potreby prognózovania je možné použiť v spojení s JMNŠ, teda s metódou analýzy časového radu v časovej doméne. Využíva sa fakt, že medzi jednotlivými metódami neexistuje pevná hranica a metódy sa vzájomne dopĺňajú. Pre prvotnú analýzu radu sa použije spektrálna analýza, tzn. pomocou periodogramu sa určia jeho významné sezónne alebo cyklické zložky a rad sa vyjadrí ako lineárna kombinácia periodických funkcií. Vzniknutý model sa následne kvantifikuje s využitím JMNŠ. V prípade, že výsledky verifikácie modelu sú pozitívne a model je významný, pre nové hodnoty časovej premennej je možné vypočítať prognózy.
Fourierova reprezentácia časového radu
Podstatou spektrálnej analýzy je vyjadrenie časového radu s dĺžkou N ako lineárnej kombinácie periodických funkcií s rôznymi frekvenciami a amplitúdami. Rad pritom nemusí byť periodický, resp. jeho periodicita nemusí byť na prvý pohľad badateľná. V praxi sa najčastejšie využívajú na takúto transformáciu radu funkcie sínus a kosínus.
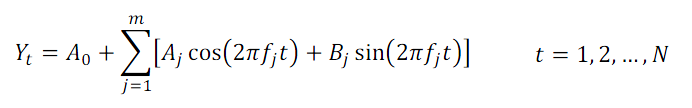
A0 je konštanta,
m = N/2, pre N párne, resp. m = (N – 1)/2, pre N nepárne,
Aj, Bj sú amplitúdy jednotlivých cyklov,
fj je postupnosť tvorená Fourierovými frekvenciami, t.j. fi = {1/N, 2/N, …, k/N}, pre k = N/2, ak N je párne, resp. k = (N – 1)/2, ak N je nepárne.
Tento vzťah sa nazýva Fourierova reprezentácia časového radu. Frekvencia fj sa udáva v cykloch za jednotku času. Jej ekvivalentom v radiánoch je uhlová frekvencia ωj =2πfj.
Tento model je možné aplikovať na akýkoľvek časový rad, ktorý nemusí nevyhnutne obsahovať cyklické zložky.
Príklad použitia spektrálnej analýzy a periodogramu
Z predchádzajúceho vzorca uvažujme o príklade, kde m=3 a N=100. Pre t=1..100 generujeme 3 rady:
Yt1 = 2 cos(2πt 6/100) + 3 sin(2πt 6/100)
Yt2 = 4 cos(2πt 10/100) + 5 sin(2πt 10/100)
Yt2 = 6 cos(2πt 40/100) + 7 sin(2πt 40/100)
Z týchto radov zostavíme model:
Yt = Yt2 + Yt2 + Yt3
V R zadefinujeme predchádzajúci model ako:
#definujeme t z rozsahu 1 až N(100)
t = 1:100
#definovanie radov
yt1 = 2*cos(2*pi*t*6/100) + 3*sin(2*pi*t*6/100)
yt2 = 4*cos(2*pi*t*10/100) + 5*sin(2*pi*t*10/100)
yt3 = 6*cos(2*pi*t*40/100) + 7*sin(2*pi*t*40/100)
#definovanie modelu
yt = yt1 + yt2 + yt3
#vykreslenie grafov
par(mfrow=c(2,2))
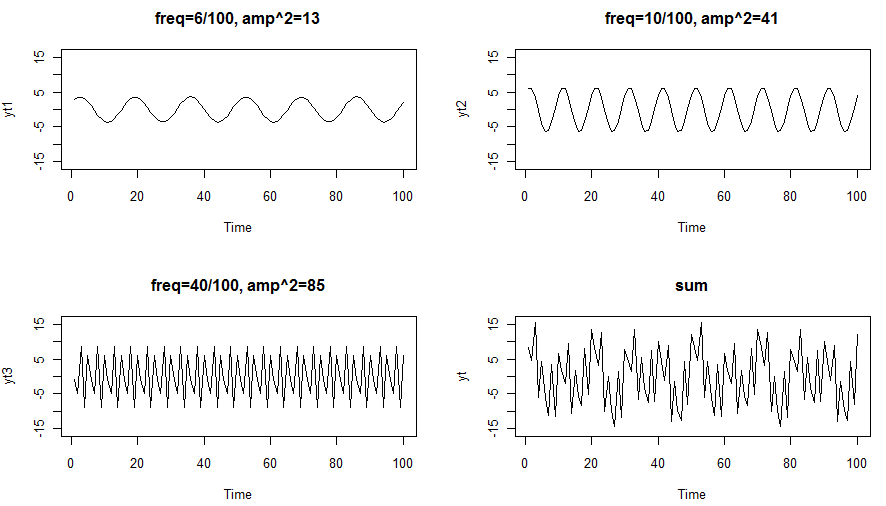
plot.ts(yt1, ylim=c(-16,16), main="freq=6/100, ampˆ2=13")
plot.ts(yt2, ylim=c(-16,16), main="freq=10/100, ampˆ2=41")
plot.ts(yt3, ylim=c(-16,16), main="freq=40/100, ampˆ2=85")
plot.ts(yt, ylim=c(-16,16), main="sum")
Periodogram môže byť vypočítaný rýchlo pomocou Rýchlej Fourierovej Transformácie(FFT). Periodogram z modelu Yt v R vypočítame nasledovne:
P = abs(2*fft(yt)/100)ˆ2
f = 0:50/100
plot(f, P[1:51], type="o", xlab="frequency", ylab="periodogram")
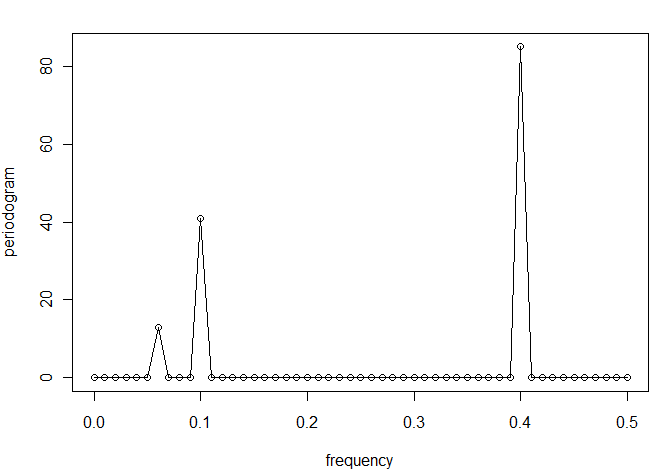
Tento periodogram jednoznačne určuje zložky Yt1, Yt2 a Yt3. Ako môžme vidieť, jednotlivé výšky sú:
P(6/100) = 13, P(10/100) = 41, P(40/100) = 85
Keby sme považovali dáta Yt za farbu, vytvorenú z primárnych farieb Yt1, Yt2 a Yt3 rôznej intenzity(amplitúdy), tak potom môžme chápať periodogram ako dekompozíciu farby Yt na jej primárne farby(spektrum). Preto termín spektrálna analýza.
Zdroje:
Jurčo, M.: DIPLOMOVÁ PRÁCA: Modelovanie sezónnosti v ekonomických procesoch s využitím aplikácie Open Source. 2010
Shumway, R., Stoffer D.:Time Series Analysis and Its Applications With R Examples. New York: Springer Science + Business Media, 2011 ISBN 978-1-4419-7864-6