SV regresia

Teória

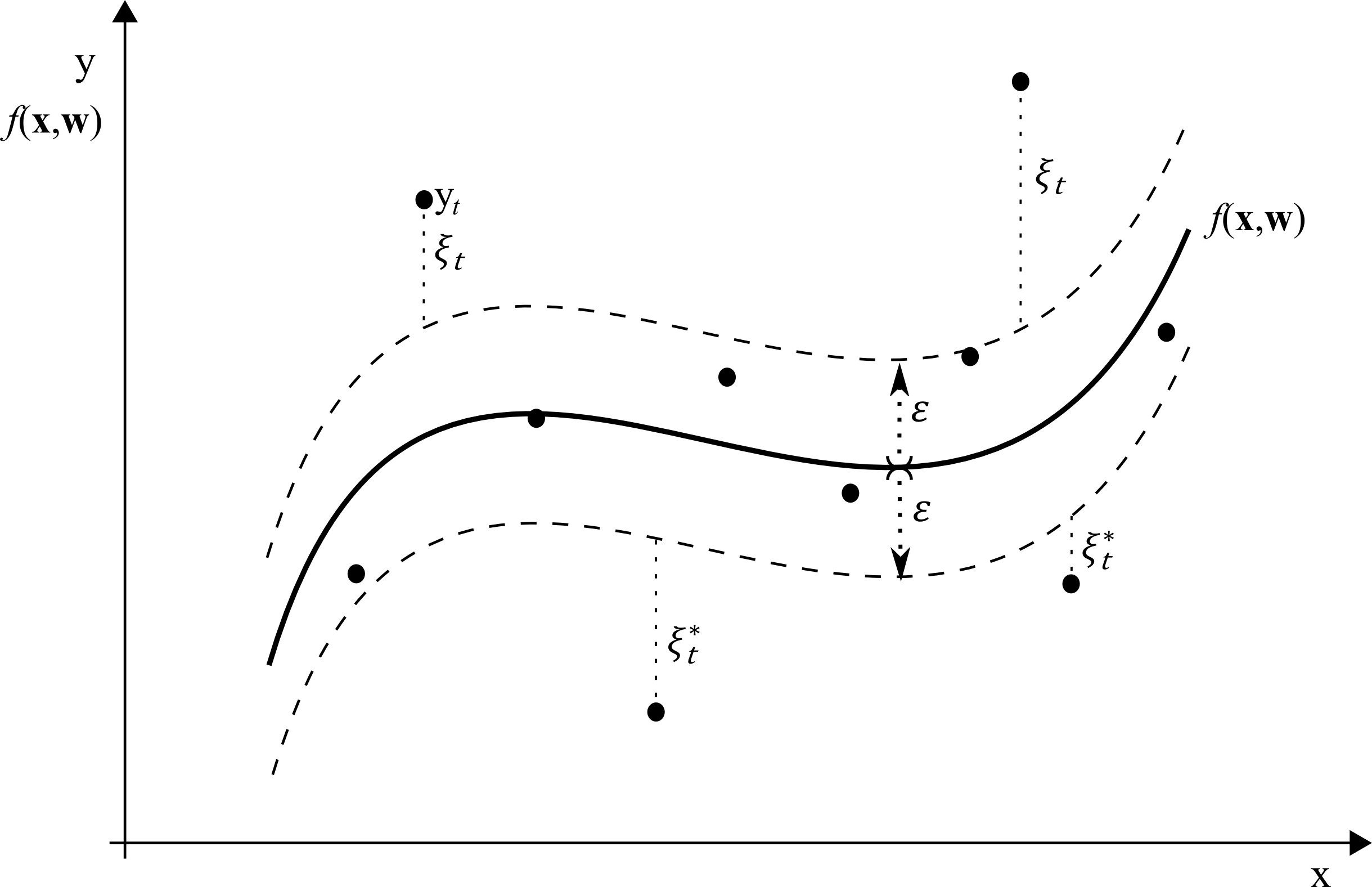
SV regresia je metóda…

svmNelinRegGrafSVM v R

V Rku je metóda SVM implementovaná vo viacerých knižniciach: kernlab, klaR, svmpath, e1071. V nasledujúcich častiach si predstavíme použitie knižnice e1071, kde je SVM implementovaná podľa azda najpoužívanejšej knižnice pre túto metódu LIBSVM. Začneme načítaním knižnice:

library(e1071)

Na trénovanie modelu slúži funkcia svm s nasledujúcimi parametrami a ich defaultnými hodnotami:

svm(x, y = NULL, scale = TRUE, type = NULL,
kernel = "radial",degree = 3, gamma = if (is.vector(x)) 1 else 1 / ncol(x),
coef0 = 0, cost = 1, nu = 0.5, class.weights = NULL, cachesize = 40,
tolerance = 0.001, epsilon = 0.1, shrinking = TRUE, cross = 0,
probability = FALSE, fitted = TRUE, ...,subset,
na.action = na.omit)

Vychádzajúc z teórie, najdôležitejšia je voľba týchto parametrov:

  • formula … symbolický popis modelu,
  • x …………….vektor alebo matica hodnôt vysvetľujúcich premenných,
  • y …………….vektor hodnôt vysvetľovanej premennej,
  • data ………objekt typu data.frame, v ktorom sa nachádzajú hodnoty premenných x a y. Ak nie je zadaný, vezmú sa z aktuálneho pracovného prostredia,
  • type.……..typ SVM metódy; možnosti výberu sú:
    • C-classification,
    • nu-classification,
    • one-classification,
    • eps-regression,
    • nu-regression, pričom prvé tri sú určené na klasifikáciu a ostatné dve na regresiu. SVR tak, ako je popísaná v teórii, je typ eps-regression,
  • kernel……typ kernel funkcie použitej v modeli; možnosti:
    • linear,
    • polynomial,
    • radial basis,
    • sigmoid,
  • cost………penalizačná konštanta, označovaná v teórii ako C,
  • epsilon.…konštanta v ε - ignorujúcej stratovej funkcii, šírka ε – pásu.
  • V závislosti od zvolenej kernel funkcie sa ďalej dajú nastaviť parametre tejto funkcie pomocou parametrov degree  pre polynomickú funkciu, gamma pre všetky funkcie okrem lineárnej a coef0 pre polynomickú a sigmoidnú funkciu.

Ďalšia funkcia v knižnici e1071, ktorá súvisí s metódou SVM, je funkcia tune, slúžiaca na optimalizáciu parametrov modelu podľa chyby MSE. Na predikciu hodnôt podľa vytvoreného modelu slúži funkcia predict.svm.

Príklad

Použité dáta sú dostupné tu. Pre potreby príkladu predpokladajme, že hodnoty zvoleného časového radu (y) sú závislé na jeho predchádzajúcich dvoch hodnotách (x1, x2). Dáta načítame ako typ data.frame nasledovne:

dataset

Model natrénujeme nasledujúcim príkazom:

model = svm(y~x1+x2, data= dataset,  type="eps-regression",
kernel="linear",cost=1, epsilon=0.01)

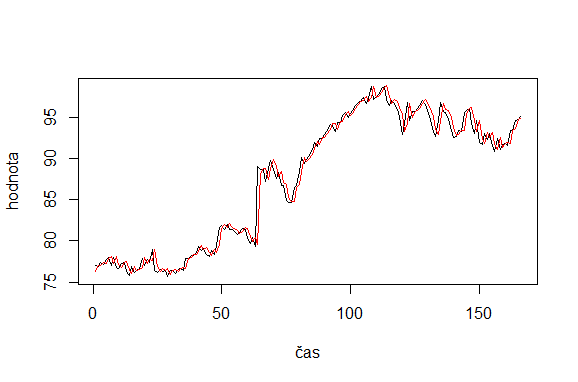
Následne môžeme získať predikcie z existujúceho modelu, z ktorých môžeme napríklad vypočítať kritérium RMSE, alebo ich vykresliť do grafu:

predictions=predict(model, dataset)
rmse=sqrt(mean((data$y-predictions)^2))
plot(dataset$y, type='lines')
lines(predictions, col='red')

SVRplot

Parametre modelu môžeme samozrejme meniť. Najpodstatnejšia je voľba parametrov epsilon a cost a voľba kernel funkcie. V závislosti od zvolenej kernel funkcie je možná voľba ďalších parametrov. Parametre môžeme optimalizovať napríklad pomocou preddefinovanej funkcie tune nasledovne:

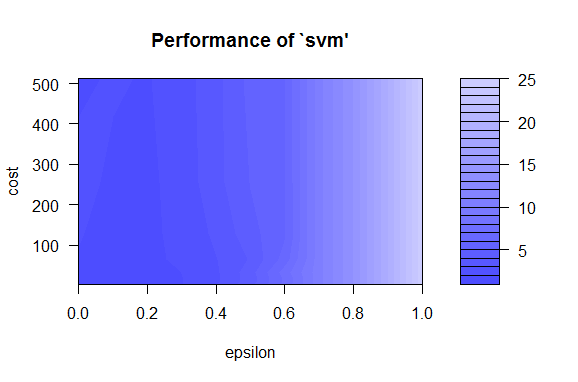
tunedModel ranges = list(epsilon = seq(0,1,0.1), cost = 2^(2:9)) )
print(tunedModel)
plot(tunedModel)

smrTunedResult

SVRTunedPlot

Funkciu môžeme spustiť aj viackrát pre hodnoty parametrov, pri ktorých má kritérium najlepšie hodnoty (najtmavšia oblasť na grafe) a zvoliť si menšiu zmenu ľubovoľného parametra. Funkcia tune optimalizuje model podľa kritéria MSE vypočítaného z množiny, na ktorej je model trénovaný. Pre väčšiu voľnosť vo výbere kritéria optimalizácie a použitej množiny na jeho výpočet si môžeme napísať vlastný kód:

trainset=dataset[1:100,]
testset=dataset[101:166,]
costs= 2^seq(from=-3, to=5, by=2)
gammas= 2 ^ seq(from=-4, to=4, by=1)
rmses = matrix(nrow= length(costs), ncol= length(gammas))
for(i  in 1:length(gammas)){
for(j  in 1:length(costs)){
model = svm(y~x1+x2, data= trainset,  type="eps-regression",
kernel="radial",cost=costs[j],gamma=gammas[i])
predictions=predict(model, testset)
rmses[j,i]=sqrt(mean((dataset$y-predictions)^2)) }}

Do tabuľky rmses sa nám uložili hodnoty kritéria pre modely so všetkými kombináciami hodnôt zvolených parametrov. Tabuľka poskytuje rovnakú informáciu ako graf pri funkcii tune. Rozsah a interval testovaných hodnôt pre rôzne parametre si môžu byť opäť ľubovoľne modifikované, rovnako aj kritérium, ktorého hodnotu chceme pre každý model získať.

Zdroje:
Package e1071 [4.6.2015]
Metoda nejmensich ctvercu [4.6.2015]
Kecman, V.: Learning and soft computing. MIT Press, 2001. ISBN: 0-262-11255-8
Slavík, M.: DIPLOMOVÁ PRÁCA: Predikcie finančných dát v investičnom rozhodovaní. 2015

Comments are closed.