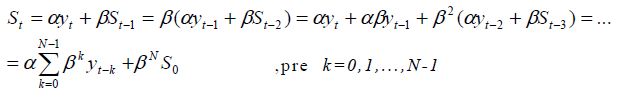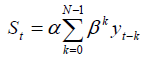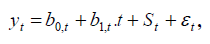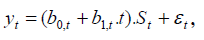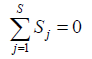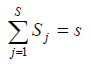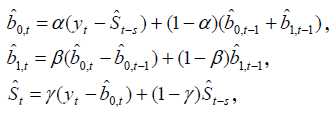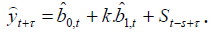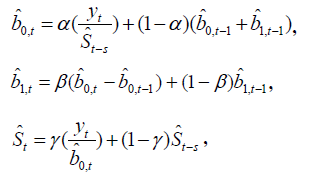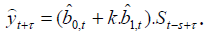Metóda exponenciálneho vyrovnávania je najviac používanou prognostickou metódou pre jej výpočtovú jednoduchosť a predovšetkým pre schopnosť rýchleho reagovania na posledné zmeny hodnôt časového radu. Metodika zohľadňuje minulý vývoj sledovanej veličiny pomocou jej vážených priemerov.
Definujeme exponenciálne vyrovnávanie v čase t pomocou nasledovného vzorca:
Kde:
St – je exponenciálny priemer v čase t
α – vyrovnávajúca konštanta z intervalu <0,1>; ß=1-α
N – dĺžka časového radu
k – vek pozorovaní
Ak je časový rad dostatočne dlhý, člen ßNS0 z posledného výrazu možno vynechať. Potom vzorec
je vážený súčet všetkých členov ČR s exponenciálne klesajúcimi váhami.
Voľba vyrovnávajúcej konštanty
Voľbou vyrovnávacej konštanty α je určovaná rýchlosť prispôsobovania ďalšej predpovede k aktuálnej chybe predpovede. Ak je α vysoké, v novej predpovedi alebo v novom odhade je zahrnutá veľká časť posledného pozorovania. Ak α je volené blízko nuly, nová predpoveď sa bude takmer zhodovať s predchádzajúcou a vplyv poslednej aktuálnej veličiny je potlačený . Znamená to, ak budeme požadovať, aby predpovede modelovanej veličiny boli stabilné a náhodné chyby nebol i extrémne rozdielne, potom budeme voliť nízku hodnotu α. Ak budeme požadovať, aby nové odhady zahŕňali rýchlu odozvu na poslednú zmenu, budeme voliť α veľké. V rôznych zdrojoch odbornej literatúry možno nájsť odporúčanie, aby α nepresahovala hodnotu 0,3.
- bez sezónnosti
- konštantný trend – Brownovo jednoduché exponenciálne vyrovnávanie
- lineárny trend – Brownovo dvojité exponenciálne vyrovnávanie, Holtovo exp. vyrovnávanie (dve vyrovnávajúce konštanty)
- kvadratický trend – trojité exponenciálne vyrovnávanie
- so sezónnou zložkou
- Holt-Winter
Holt-Winter
Pri použití Holt-Winter-ovho exponenciálenho vyrovnávania sa predpokladá, že v čase t=1,2,3,…,T, je možné časový rad rozdeliť na lokálne lineárne trendy s konštantou alebo multiplikatívnou sezónnosťou.
- Aditívny model
- Multiplikatívny model
kde:
b0 – parameter úrovne lineárneho modelu
b1 – parameter smernice lineárneho modelu
ε0 – náhodná zložka
t – časová premenná
St – sezónny priemer/ sezónnz index v čase t, pričom musí platiť:
pre sezónne priemery,
pre sezónne indexy.
V modeli používame tri vyrovnávajúce konštanty α, β, γ.
Vyrovnávajúce rovnice:
- Aditívny model
a prognózovanie má tvar
- Multiplikatívny model
a prognózovanie má tvar
Exponenciálne vyrovnávanie v R
Najznámejšia je funkcia HoltWinters, ktorá dokáže pracovať so sezónnymi aj nesezónnzmi dátami. Táto funkcia je obsiahnutá v základných balíkoch, preto nie je potrebné inštalovať a načitávať žiadne balíky.
HoltWinters(x, alpha = NULL, beta = NULL, gamma = NULL, seasonal = c("additive", "multiplicative"))
Parametre funkcie:
- x – dáta časového radu
- alpha, beta, gamma – vyrovnávajúce konštanty
- seasonal – defaultne “additive”, pre multiplikatívny sezónny model treba zadať “multiplicative”. Tento parameter naberá účinnosť, len ak je parameter gamma nenulový
Príklad:
Nesezónne dáta
#načítanie dát
Dáta použité v tomto príklade nájdete tu: Odkazy na použité a reálne dáta
#zavolanie funkcie na exponenciálne vyrovnávanie
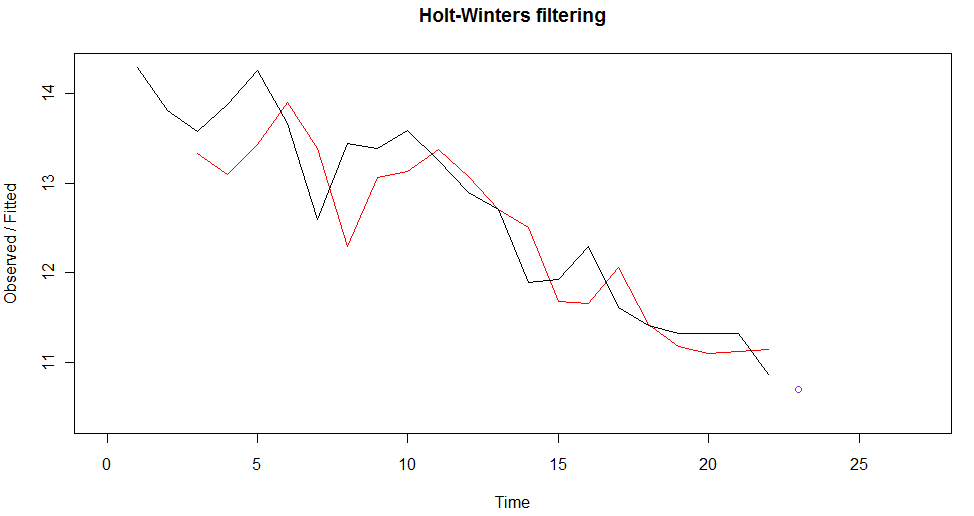
yt.hw = HoltWinters(yt, gamma=FALSE)
#vykreslenie výstupu z funkcie HoltWinters so zmenenými mierkami, aby sa tam potom zmestila ja prognóza
plot(yt.hw, xlim=c(0, length(yt)+5), ylim=c(min(yt)-0.5, max(yt)))
#výpočet prognózy
yt.hw.pred = predict(yt.hw, n.ahead=1)
#zakreslenie prognózy do existujúceho grafu
lines(yt.hw.pred, type="p", col="purple")
Sezónne dáta
#načítanie dát
Dáta použité v tomto príklade nájdete tu: Odkazy na použité a reálne dáta
#dáta konvertované do formátu potrebného na vstupe do funkcie HoltWinters pre sezónne dáta
#dáta sú mesačné(freq=12) a začínajú rokom 1956
yt<-ts(yt,start=1956,freq=12)
#zavolanie funkcie na exponenciálne vyrovnávanie
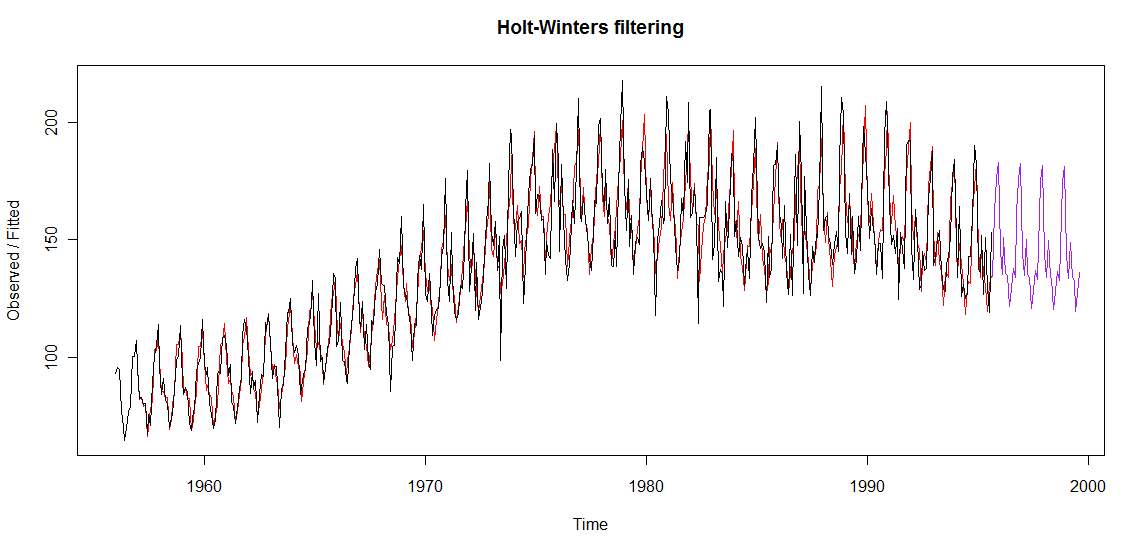
yt.hw = HoltWinters(yt)
#vykreslenie výstupu z funkcie HoltWinters so zmenenými mierkami, aby sa tam potom zmestila ja prognóza
plot(yt.hw, xlim=c(1956, 1999))
#výpočet prognózy
yt.hw.pred = predict(yt.hw, n.ahead=48)
#zakreslenie prognózy do existujúceho grafu
lines(yt.hw.pred, col="purple")
Odhad modelu HW, ktorý je v grafe červenou čiarou a využívame ho na výpočet chybovosti získame:
c(yt.hw$fitted[,"xhat"])
Zdroje:
Polívka, L.: DIPLOMOVÁ PRÁCA: Moderné prognostické metódy v modelovaní podnikových procesov. 2010
Zucchini, W., Nenadi, O., :Time Series Analysis with R -Part I [4.6. 2015]