Simultánne modely

Ak existuje niekoľko endogénnych premenných, ktoré vystupujú v úlohe tak vysvetľujúcich ako aj vysvetľovaných premenných, súčasne determinované sústavou lineárnych či nelineárnych vzťahov jedná sa o ekonometrický model simultánnych rovníc (EMSR):

• aspoň jedna rovnica obsahuje viac ako jednu endogénnu premennú
• celkový počet endogénnych premenných je rovný počtu rovníc
• v EMSR existujú spätné väzby medzi endogénnymi premennými časovo neoneskorenými
• MNŠ (až na špeciálne prípady) neposkytuje nestranné ani konzistentné odhady parametrov (existencia nestochastických aj stochastických endogénnych premenných)

Príklad:

Je daný jednoduchý makroekonomicky model simultánnych rovníc (MSR). Zostavte štrukturálnu formu, interpretačný zápis, kvantifikačný zápis a redukovanú formu EM. Zistite, čí je možný jednoznačný výpočet parametrov štrukturálnej formy modelu z redukovanej formy modelu. C_t = a₀ + a₁Y_t + a₂C_t-1 + u_t1 Y_t = b₀ + b₁I_t + b₂M_t + u_t2 I_t = c₀ + c₁r_t + c₂I_t-1 + u_t3 G_t = Y_t – C_t – I_t C_t je je konečná spotreba v období t Y_t je HDP v období t I_t sú hrubé investície v období t r_t je úroková miera v období t M_t je ponuka peňazí v období t G_t sú vládne výdavky v období t.

Dáta použité v tomto príklade nájdete tu: Odkazy na použité a reálne dáta

Riešenie v R

V prvom rade je dôležité kategorizovať premenné na endogénne, exogénne, časovo posunuté a predeterminované. Endogénne premenné sú všetky premenné nachádzajúce sa na ľavej strane rovníc. Sú to premenné: C_t, Y_t, I_t, G_t Exogénne premenné sú tie, ktoré vystupujú ako nezávislé. V tomto prípade sú to: M_t, r_t, Lokujúca konštanta(absolútny člen) Časovo posunuté premenné, sú tie, ktoré sú posunuté o časové obdobie, v našom prípade sú to premenné: C_t-1, I_t-1 Predeterminované premenné sú všetky časovo posunuté endogénne premenné a exogénne premenné, teda sú to: M_t, r_t, LK, C_t-1, I_t-1 Rovnice si ešte môžeme rozdeliť na stochastické a identity. Stochastické rovnice sú všetky tie, ktoré obsahujú náhodnú zložku. Stochastické: C_t = a₀ + a₁Y_t + a₂C_t-1 + u_t1 Y_t = b₀ + b₁I_t + b₂M_t + u_t2 I_t = c₀ + c₁r_t + c₂I_t-1 + u_t3 Identita: (Bilančná rovnica) G_t = Y_t – C_t – I_t

Štrukturálna forma

Na zostavenie štrukturálnej formy budeme vzchádzať z rovníc, ktoré máme v zadaní a to tak, že každej rovnici odhadneme parametre a tak zostavíme štrukturálnu formu. V programe R na to použijeme knižnicu systemfit Vzhľadom k tomu, že sa v medizi premennými nachádzajú aj časovo posunuté premenné, tak budeme počítať až od druhého údaju pre všetky premenné, aby sme udržali konzistentnosť dát. Ct<-c(167.5,156.2,167.2,169.8,188.8,186.5,195.7,187.6,203.6) Yt<-c(321.8,345.2,334.4,319.9,343,367.9,350.3,339.1,360.7) Ct1<-c(144.1,167.5,156.2,167.2,169.8,188.8,186.5,195.7,187.6) Yt<-c(321.8,345.2,334.4,319.9,343,367.9,350.3,339.1,360.7) It<-c(3.14,3.43,3.41,3.31,3.12,3.11,3.02,2.96,2.93) Mt<-c(770.2,792.7,876.4,856.6,888.1,959.8,1012.3,1014.3,1053.9) It<-c(3.14,3.43,3.41,3.31,3.12,3.11,3.02,2.96,2.93) rt<-c(2.05,2.89,2.85,1.24,2.8,3.36,2.48,2.11,1.17) It1<-c(2.81,3.14,3.43,3.41,3.31,3.12,3.11,3.02,2.96) Zo zadaných údajov vytvoríme systém rovníc: (4. rovnica je identita, takže pre túto rovnicu nepočítame regresiu) system <- list( rovnica1 = Ct~Yt+Ct1, rovnica2 = Yt~It+Mt, rovnica3 = It~rt+It1 ) Nakoniec vypočítame regresie library(systemfit) # načítame knižnicu systemfit( system, “OLS”) Výsledok: systemfit results method: OLS Coefficients: rovnica1_(Intercept) rovnica1_Yt rovnica1_Ct1 22.1711564 0.1845999 0.5464803 rovnica2_(Intercept) rovnica2_It rovnica2_Mt 187.8270240 13.8588376 0.1213295 rovnica3_(Intercept) rovnica3_rt rovnica3_It1 1.4680731 0.0490185 0.5012506 Štruktúrovaný tvar bude vyzerať nasledovne: C_t = 22,1712 + 0,1846.Y_t + 0,5465.C_t-1 + u_t1 Y_t = 187.8270 + 13.8588.I_t + 0.1213.M_t + u_t2 I_t = 1,46807 + 0,04902.r_t + 0,50125.I_t-1 + u_t3 G_t = Y_t – C_t – I_t

Interpretačná forma

Na zostavenie interpretačnej formy budeme vychádzať zo štrukturálnej formy a to tak, že všetky hodnoty okrem náhodnej zložky sa presunú na ľavú stranu rovnice. Zostavujú sa pritom tak, že najskôr idú za sebou endogénne premenné a potom idú predetreminované premenné. Interpretačná forma bude vyzerať nasledovne: 1.C_t – 0,1846.Y_t + 0.I_t + 0.G_t + 0.r_t + 0.M_t – 0,5465.C_t-1 + 0.I_t-1 – 22,1712 = 1.u_t1 0.C_t + 1.Y_t – 13.8588.I_t + 0.G_t + 0.r_t – 0.1213.M_t + 0.C_t-1 + 0.I_t-1 – 187.8270 = 1.u_t2 0.C_t + 0.Y_t + 1.I_t + 0.G_t – 0,04902.r_t + 0.M_t + 0.C_t-1 – 0,50125.I_t-1 – 1,46807 = 1.u_t3 1.C_t – 1.Y_t + 1.G_t + 0.r_t + 0.M_t + 0.C_t-1 + 0.I_t-1 + 0 = 0.u_t4

Kvantifikačný tvar

Je daný tvarom YA+XB=U, pričom matica Y je matica pozorovaní endogénnej premennej, matica X, je matica pozorovaní predeterminovaných premenných, matica A je matica parametrov endogénnych premenných, matica B je matica predeterminovaných premenných a matica U je matica náhodných zložiek. Matica Y:

Ct	Yt	It	Gt
144,1	302,2	2,81	3,39
167,5	321,8	3,14	4,04
156,2	345,2	3,43	7,34
167,2	334,4	3,41	7,95
169,8	319,9	3,31	2,43
188,8	343	3,12	6,50
186,5	367,9	3,11	10,24
195,7	350,3	3,02	6,92
187,6	339,1	2,96	4,93
203,6	360,7	2,93	3,90

Matica X:

rt	Mt	Ct-1	It-1	LK
1,84	731,4	-	-	1
2,05	770,2	144,1	302,2	1
2,89	792,7	167,5	321,8	1
2,85	876,4	156,2	345,2	1
1,24	856,6	167,2	334,4	1
2,8	888,1	169,8	319,9	1
3,36	959,8	188,8	343	1
2,48	1012,3	186,5	367,9	1
2,11	1014,3	195,7	350,3	1
1,17	1053	187,6	339,1	1

Matica A:

1              0            0    1   Ct

-0,1846    1             0   -1   Yt

0           -13.8588    1    1   It

0             0            0    1   Gt

Matica B:

0            0             -0,04902  0   rt

0          -0.1213       0             0   Mt

-0,5465  0              0             0   Ct-1

0            0            -0,50125    0   Lt-1

-22,1712 -187.8270 -1,46807   0   Lk

Identifikácia viacrovnicových modelov

Vzhľadom k tomu, že problém identifikácie viacrovnicových modelov, je kľúčový pri výbere vhodnej metódy odhadu parametrov, je tento proces veľmi dôležitý. Celá identifikácia sa robí pomocou rozmerovej skúšky. Túto skúšku môžeme zapísať vzťahom K-k>=g-1, pričom K je počet všetkých predeterminovaných premenných, k je počet predeterminovaných premenných v konkrétnej rovnici a g je počet endogénnych premenných v konkrétnej rovnici. Rozmerovú skúšku robíme len pre stochastické rovnice, pretože identita je považovaná za presne identifikovanú rovnicu. Ak platí že K-k=g-1, tak je potom rovnica presne identifikovaná. Ak je K-k>g-1, tak potom je rovnica preidentifikovaná. Ak je K-k neidentifikovaná, alebo nedostatočne identifikovaná. V našom prípade si môžeme vytvoriť tabuľku, podľa ktorej rozhodneme o identifikácií rovníc: Rovnice: C_t = a₀ + a₁Y_t + a₂C_t-1 + u_t1 Y_t = b₀ + b₁I_t + b₂M_t + u_t2 I_t = c₀ + c₁r_t + c₂I_t-1 + u_t3 G_t = Y_t – C_t – I_t Tabuľka:

	k	K	G
1.Rovnica	5	2	2	3>1	Preidentifikovaná
2.Rovnica	5	2	2	3>1	Preidentifikovaná
3.Rovnica	5	2	1	2>0	Preidentifikovaná
4.Rovnica	5	2	1	2>0	Presne identifikovaná

Záver: Vzhľadom k tomu, že vo všeobecnosti je model taký, aká je jeho najhoršia rovnica, v našom prípade je model PREIDENTIFIKOVANÝ. Z tohto vyplýva, že nie je možné jednoznačný výpočet parametrov štrukturálnej formy modelu z redukovanej formy modelu.

Voľba odhadovej metódy pre kvantifikáciu parametrov

Konkrétna voľba odhadovej metódy pre kvantifikáciu parametrov jednotlivých stochastických rovníc modelu je závislá od základných charakteristík modelu ako je :

• tvar matice parametrov endogénnych časovo neoneskorených premenných A
• identifikácia modelu a rovníc (presná identifikácia, preidentifikácia, neidentifikácia modelu).

Ak prihliadneme súčasne k obom charakteristikám môžeme zostaviť jednoduché rozhodovacie schéma výberu vhodných metód odhadu parametrov viacrovnicových ekonometrických modelov.

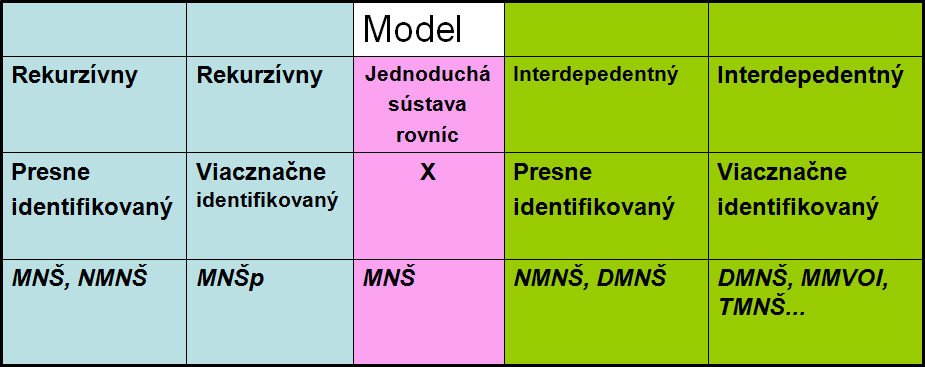
MNŠ…metóda najmenších štvorcov
NMNŠ…nepriama metóda najmenších štvorcov
MNŠp….. metóda najmenších štvorcov postupne aplikovaná
DMNŠ….dvojstupňová metóda najmenších štvorcov
MMVOI…metóda maximálnej vierohodnosti s obmedzenými informáciami
TMNŠ… trojstupňová metóda najmenších štvorcov

Odhad parametrov

Na odhad parametrov v prostredí R je najlepšie použitie knižnice SYSTEMFIT. Táto knižnica bola použitá aj v predchádzajúcom príklade na výpočet JMNŠ. Táto knižnica obsahuje funkcie na výpočet lineárnych a nelineárnych rovníc pomocou JMNŠ(OLS), váženej MNŠ(WLS), dvojstupňovej MNŠ(2SLS), váženej dvojstupňovej MNŠ(W2SLS), trojstupňovej MNŠ(3SLS) a iných.

Odhad parametrov pomocou dvojstupňovej metódy najmenších štvorcov

Keď už máme zadané jednotlivé parametrea taktiež aj zadefinovaný systém, tak už je potrebné len zadefinovať predeterminované premenné systému:

inst <- ~Ct1 + Mt + rt + It1

A môžme počítať odhad parametrov:

systemfit( system, “2SLS”, inst=inst)

Coefficients:
rovnica1_(Intercept) rovnica1_Yt rovnica1_Ct1
15.7726969 0.2126387 0.5280346
rovnica2_(Intercept) rovnica2_It rovnica2_Mt
256.0768303 -1.5146287 0.0997859
rovnica3_(Intercept) rovnica3_rt rovnica3_It1
1.4680731 0.0490185 0.5012506

Záver

Výsledné rovnice s odhadnutými parametrami sú:
C_t = 15.7726969 + 0.2126387.Y_t + 0.5280346.C_t-1 + u_t1
Y_t = 256.0768303 – 1.5146287.I_t + 0.0997859.M_t + u_t2
I_t = 1.4680731 + 0.0490185.r_t + 0.5012506.I_t-1 + u_t3
G_t = Y_t – C_t - I_t

Zdroje:
Ekonometrický model simultánnych rovníc [4.6.2015]
Hušek, R.,Pelikán, J.: Aplikovaná ekonometria (teória a prax). Praha : Professional Publishing, 2003, ISBN 80-86419-29-0