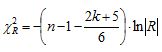Multikolinearita
Čo je multikolinearita?
Porušenie jedného z predpokladov pre náhodnú zložku a vstupných premenných ekonometrického modelu – vzájomná lineárna nezávislosť vysvetľujúcich premenných.
Možné príčiny multikolinearity:
- Zlá špecifikácia premenných,
- Malý rozsah výberového súboru.
Spôsoby zisťovania multikolinearity:
- Farrar – Glauber test,
- Variančné inflačné faktory,
- Korelačná matica,
- Vlastné čísla korelačnej matice.
Vybrané spôsoby odstránenia multikolinearity:
- vynechanie premenných, ktoré ju spôsobujú, resp. ich nahradenie inými,
- metóda hlavných komponentov,
- transformácia premenných,
- hrebeňová regresia,
- využitie apriórnych informácií o hodnotách parametrov.
Príklad:
Vzorový príklad s metódami na testovanie prítomnosti multikolinearity a jej odstránenie sa nachádza v tomto scripte.
Máme zadaný model:
yt = b0 + b1*xt1 + b2*xt2 + b3*xt3 + ut
Vypočítajte korelačnú maticu R cez normovanie premenných. Overte správnosť alebo nesprávnosť predpokladu o vysokom stupni multikolinearity. V prípade potvrdenia vysokého stupňa multikolinearity sa ju pokúste odstrániť vhodnou metódou.
Riešenie:
Najprv je potrebné načítať údaje z príkladu, v našom prípade Yt, Xt1, Xt2, Xt3.
| 2. Vytvoríme si korelačnú maticu pomocou funkcie cor() |
Ukázať |
Korelačná matica (correlation matrix) je matica párových korelačných koeficientov pre všetky dvojice vysvetľujúcich premenných. Maticu vysvetľujúcich premenných získame pomocou funkcie cbind(). Výslednú korelačnú maticu si uložíme do premennej kor_mat.
vys_mat=cbind(Xt1,Xt2,Xt3)
# matica vysvetľujúcich premenných
kor_mat=cor(vys_mat)
# korelačná matica
|
| 3. Teraz otestujeme významnosť stupňa multikolinearity pomocou Farrar – Glauber testu. |
Ukázať |
Postup Farrara – Glaubera navrhuje významnosť multikolinearity preskúmať na základe aproximatívnej transformácie hodnoty korelačnej matice na veličinu s chi2 rozdelením. Vzorec na výpočet je:
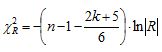
Na výpočet Farrar-Glauber testu si môžeme vytvoriť vlastnú funkciu. Postup vytvorenia vlastnej funkcie je podrobne popísaný v časti R Cran / Vytvorenie funkcie, takže tu si už iba zadefinujeme všeobecnú funkciu, ktorú si nazveme napríklad fgtest.
fgtest = function(vn,cor_mat)
{
dof_cor=dim(cor_mat)[1] #počet stupňov voľnosti
chi_sq_cal=((-1)*(length(vn)-1-(2*dof_cor+5)/6)*log(det(cor_mat))) #chi^2
chi_sq_tab=qchisq(0.95,1/2*dof_cor*(dof_cor-1)) #chi^2 tab hodnota
if(chi_sq_cal>chi_sq_tab) #ak je vypočítaná väčšia ako tab, zamietam h0
cat("multikolinearita je významná")
else
cat("multikolinearita nie je významná")
}
Funkciu spustíme príkazom názov funkcie s potrebnými parametrami. Prvý parameter je premenná Xt1 (funkcia z nej získa počet pozorovaní), druhý parameter je korelačná matica, v našom prípade kor_mat. Takže spustenie funkcie v našom prípade vyzerá takto:
fgtest(Xt1,kor_mat)
Funkcia vypočíta hodnotu χ2 a ak tá je väčšia ako hodnota χ2 tabuľková (α=0,05), zamietne hypotézu H0 a príjme hypotézu H1 a vypíše “multikolinearita je prítomná”.
|
Odstránenie multikolinearity
V prípade prítomnej multikolinearity ju môžeme odstrániť pomocou Metódy hlavných komponentov (Principal components analysis – PCA) – funkcia princomp() alebo cez vlastné vektory.
| MHK pomocou funkcie princomp() |
Ukázať |
kor=princomp(cbind(Xt1,Xt2,Xt3),cor=TRUE)
mhk<-kor$scores
mhk
# vypisanie matice hlavných komponentov
|
Comp.1 |
Comp.2 |
Comp.3 |
| [1,] |
-2.60069198 |
-0.06042369 |
-0.060960241 |
| [2,] |
-2.16620497 |
-0.53341589 |
0.067693422 |
| [3,] |
-1.57505903 |
0.32416004 |
0.050637316 |
| [4,] |
-0.90796689 |
0.13292161 |
0.005322251 |
| [5,] |
-0.08580467 |
0.12951905 |
-0.155971968 |
| [6,] |
0.34921196 |
0.03743760 |
-0.037228510 |
| [7,] |
0.70722316 |
0.23234899 |
0.129594319 |
| [8,] |
1.45185034 |
0.13502849 |
0.026289677 |
| [9,] |
2.11894248 |
-0.05620993 |
-0.019025389 |
| [10,] |
2.70849958 |
-0.34136628 |
-0.006350878 |
Pre odstránenie multikolinearity je potrebné urobiť regresiu z hlavných komponentov. Najskôr je potrebné transponovať maticu hlavných komponentov a transponovanú maticu nazveme napr. MHKtran. Následne je potrebné vytvoriť inverznú maticu inv a normované Yt, ktoré nazveme nYt
MHKtran = t(mhk)
inv = solve(MHKtran %*% mhk)
Na výpočet štandardnej odchýlky si musíme vytvoriť vlastnú funkciu.
Nazveme ju napríklad sd1(), kedže funkcia sd() (výberová smerodajná odchýlka) sa už v R Crane nachádza.
sd1=function(a) {
p=mean(a);
n=length(a);
i=1;
b=0;
while(i<=n){
b[i]=c((a[i]-p)^2)
i=i+1
};
return(sqrt(sum(b)/n))
}
Teraz vypočítame normované nYt a koeficienty regresnej funkcie.
nYt=(Yt-mean(Yt))/sd1(Yt)
b = inv %*% MHKtran %*% nYt
b
Koeficienty regresnej funkcie (pre normované nYt) sú:
[1,] -0.5522070
[2,] -0.6381567
[3,] -2.0449395
|
| MHK cez vlastné vektory |
Ukázať |
- Cez korelačnú maticu
cor_mat = cor(cbind(Xt1,Xt2,Xt3))
# korelačná matica
eig_mat= eigen(cor_mat)
# matica vlastných vektorov
Na výpočet štandardnej odchýlky si musíme vytvoriť vlastnú funkciu.
Nazveme ju napríklad sd1(), kedže funkcia sd() (výberová smerodajná odchýlka) sa už v R Crane nachádza.
sd1=function(a) {
p=mean(a);
n=length(a);
i=1;
b=0;
while(i<=n){
b[i]=c((a[i]-p)^2)
i=i+1
};
return(sqrt(sum(b)/n))
}
Ďalej normujeme jednotlivé časové rady premenných
nXt1=(Xt1-mean(Xt1))/sd1(Xt1)
nXt2=(Xt2-mean(Xt2))/sd1(Xt2)
nXt3=(Xt3-mean(Xt3))/sd1(Xt3)
Normované rady vynásobíme maticou vlastných vektorov a dostaneme maticu hlavných komponentov
mhk=cbind(nXt1,nXt2,nXt3) %*% eig_mat$vectors
mhk
|
Comp.1 |
Comp.2 |
Comp.3 |
| [1,] |
-2.60069198 |
-0.06042369 |
-0.060960241 |
| [2,] |
-2.16620497 |
-0.53341589 |
0.067693422 |
| [3,] |
-1.57505903 |
0.32416004 |
0.050637316 |
| [4,] |
-0.90796689 |
0.13292161 |
0.005322251 |
| [5,] |
-0.08580467 |
0.12951905 |
-0.155971968 |
| [6,] |
0.34921196 |
0.03743760 |
-0.037228510 |
| [7,] |
0.70722316 |
0.23234899 |
0.129594319 |
| [8,] |
1.45185034 |
0.13502849 |
0.026289677 |
| [9,] |
2.11894248 |
-0.05620993 |
-0.019025389 |
| [10,] |
2.70849958 |
-0.34136628 |
-0.006350878 |
Pre odstránenie multikolinearity je potrebné urobiť regresiu z hlavných komponentov. Najskôr je potrebné transponovať maticu hlavných komponentov a transponovanú maticu nazveme napr. MHKtran. Následne je potrebné vytvoriť inverznú maticu inv a normované Yt, ktoré nazveme nYt
MHKtran = t(mhk)
inv = solve(MHKtran %*% mhk)
nYt=(Yt-mean(Yt))/sd1(Yt)
b = inv %*% MHKtran %*% nYt
b
Koeficienty regresnej funkcie (pre normované nYt)sú:
[1,] -0.5522070
[2,] -0.6381567
[3,] -2.0449395
|
Zdroje:
Multikolinearita a jej diagnostika [4.6.2015]
Marček, D., Marček, M., Pančíková, L.: Ekonometria a soft computing. Žilina: EDIS, 2008 ISBN 978-80-8070-746-0