Ekonometria
Máme dané hodnoty časových radov Yt, Xt1, Xt2 , ktoré sa menia v čase t. Zistite vzťah závislosti Yt od Xt1 a Xt2, overte predpoklady o náhodnej zložke (autokorelácia, heteroskedasticita, multikolinearita) a v prípade potreby upravte model na vhodnejší.
Yt<-c(210, 212, 214, 212, 215, 216, 217, 218, 220, 222, 223, 224, 226, 225, 228) Xt1<-c(36, 42, 62, 50, 64, 72, 75, 87, 94, 85, 104, 107, 134, 115, 150) Xt2<-c(150, 165, 162, 170, 94, 90, 90, 90, 90, 75, 75, 75, 40, 70, 15)
Lineárna regresia
Na výpočet koeficientov použijeme vlastnú funkciu:
reg = function (Yt, m)
{
regr = lm (Yt~m)
nr = nrow(m)
nc = ncol(m)
y = c()
b = c()
for (i in 1:(nc+1))
{
b[i]=regr$coef[i]
}
for (i in 1:nr)
{
ypom = 0;
for (j in 2:(nc+1))
{
ypom = ypom + b[j]*m[i,(j-1)]
}
y[i]=b[1]+ypom
}
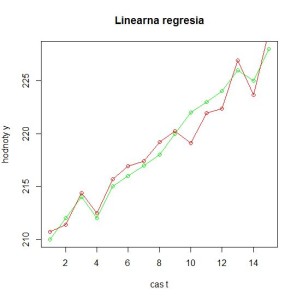
plot (Yt, type = "o", col="green",xlab="cas t",ylab="hodnoty y",
main = "Linearna regresia")
lines (y, type = "o", col="red")
cat("Linear regresion",<br />,
"--------------------------------------",<br />,
"Estimated values of Y:<br />,y,<br />,
"--------------------------------------",<br />,
"Summary from lm function:",<br />
)
summary (regr)
}
Teraz do tejto funkcie vložíme naše premenné a počkáme si na výstup.
reg(Yt,cbind (Xt1,Xt2))
Náš výstup vyzerá nasledovne:
Linear regresion
--------------------------------------
Estimated values of Y:
210.6884 211.358 214.3811 212.4747 215.6937 216.9447 217.3915 219.1785 220.2209 219.1045 221.9339 222.3806 226.9236 223.6465 229.6793
--------------------------------------
Summary from lm function:
Call:
lm(formula = Yt ~ m)
Residuals:
Min 1Q Median 3Q Max
-1.6793 -0.8087 -0.3915 0.8541 2.8955
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 207.56608 4.07526 50.933 2.15e-15 ***
mXt1 0.14891 0.02683 5.549 0.000126 ***
mXt2 -0.01492 0.01929 -0.774 0.454194
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.35 on 12 degrees of freedom
Multiple R-squared: 0.9514, Adjusted R-squared: 0.9434
F-statistic: 117.6 on 2 and 12 DF, p-value: 1.311e-08
Autokorelácia
Zistime si prítomnosť autokorelácie pomocou funkcie durbinWatsonTest(), na ktorú potrebujeme načítať knižnicu “car”. Knižnicu si vieme načítať podľa návodu tu: Knižnice
regresia = lm(Yt ~ cbind(Xt1,Xt2)) dw<-durbinWatsonTest(regresia,max.lag=1) dw
Výstup z tejto funkcie vyzerá nasledovne:
lag Autocorrelation D-W Statistic p-value
1 0.03318988 1.782994 0.36
Alternative hypothesis: rho != 0
Keďže rho je blízke 0, autokorelácia nie je prítomná.
Heteroskedasticita
Na zistenie heteroskedasticity použijeme Bartlettov test.
data<-list(Yt,Xt1,Xt2) bartlett.test(data)
Program nám vygeneruje nasledovné:
Bartlett test of homogeneity of variances
data: data
Bartlett's K-squared = 38.279, df = 2, p-value = 4.873e-09
Ftab = 9,3. B-test hodnota je väčšia ako tabuľková, teda zamietam nulovú hypotézu , z čoho vyplýva, že je tam pozitívna heteroskedasticita.
Pre odstránenie heterokedasticity potrebujeme knižnicu “Imtest”, ktorá obsahuje funkciu “gqtest”. Knižnicu si vieme načítať podľa návodu tu: Knižnice
Yt1<-1
for (i in 1:15)
{
Yt1[i]<-(Yt[i]/Xt2[i])
}
Xt<-1
for (i in 1:15)
{
Xt[i]<-(Xt1[i]/Xt2[i])
}
mat1 = cbind(Yt1, Xt, Xt2)
model1<-(Yt1 ~ Xt + Xt2)
regresia1<-lm(model1)
gqtest(regresia1, order.by = Xt2, fraction=2, data = mat1)
R nám vygeneruje nasledovné:
Goldfeld-Quandt test
data: regresia1
GQ = 0.0217, df1 = 4, df2 = 3, p-value = 0.9985
Ftab=9,3. GQ hodnota je menšia ako tabuľková, heteroskedasticitu sa nám podarilo odstrániť.
Multikolinearita
Pre zistenie multikolinearity je potrebné si najskôr vytvoriť výstupnú a korelačnú maticu z Xt1 a Xt2.
vys_mat=cbind(Xt1,Xt2) kor_mat=cor(vys_mat)
Následne si vytvoríme funkciu:
fgtest = function(vn,cor_mat)
{
dof_cor=dim(cor_mat)[1] #počet stupňov voľnosti
chi_sq_cal=((-1)*(length(vn)-1-(2*dof_cor+5)/6)*log(det(cor_mat))) #chi^2
chi_sq_tab=qchisq(0.95,1/2*dof_cor*(dof_cor-1)) #chi^2 tab hodnota
if(chi_sq_cal>chi_sq_tab) #ak je vypočítaná väčšia ako tab, zamietam h0
cat("multikolinearita je významná")
else
cat("multikolinearita nie je významná")
}
A túto funkciu aj použijeme s našimi hodnotami:
fgtest(Xt1,kor_mat)
Výstup je jednoducho zrozumiteľný:
multikolinearita je významná
Pre odstránenie multikolinearity využijeme vlastné vektory.
cor_mat = cor(cbind(Xt1,Xt2))
eig_mat= eigen(cor_mat)
sd1=function(a) {
p=mean(a);
n=length(a);
i=1;
b=0;
while(i<=n){
b[i]=c((a[i]-p)^2)
i=i+1
};
return(sqrt(sum(b)/n))
}
nXt1=(Xt1-mean(Xt1))/sd1(Xt1)
nXt2=(Xt2-mean(Xt2))/sd1(Xt2)
mhk=cbind(nXt1,nXt2) %*% eig_mat$vectors
mhk
Matica hlavných komponentov vyzerá nasledovne:
| Comp.1 | Comp.2 | |
| [1,] | 1.9440595 | 0.24092255 |
| [2,] | 2.0504516 | -0.13229224 |
| [3,] | 1.5577862 | -0.52903619 |
| [4,] | 1.9525042 | -0.39010855 |
| [5,] | 0.4262071 | 0.51360207 |
| [6,] | 0.1843776 | 0.39966779 |
| [7,] | 0.1176719 | 0.33296209 |
| [8,] | -0.1491508 | 0.06613931 |
| [9,] | -0.3047975 | -0.08950731 |
| [10,] | -0.3444838 | 0.35041317 |
| [11,] | -0.7669532 | -0.07205623 |
| [12,] | -0.8336589 | -0.13876192 |
| [13,] | -1.9935514 | -0.17957192 |
| [14,] | -1.0914752 | -0.23670931 |
| [15,] | -2.7489874 | -0.13566331 |
Po odstránení multikolinearity, poďme skontrolovať náš model a porovnať s pôvodnými hodnotami. Na vytvorenie modelu potrebujeme vybrať vektory z matice mhk, môžeme ich pomenovať A a B. Následne potrebujeme normovať pôvodné Yt na nYt. Nakoniec opäť použijeme našu funkciu reg().
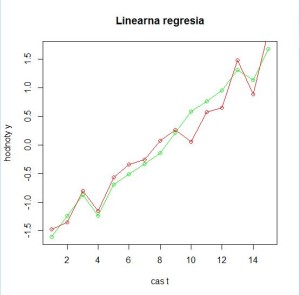
A<-mhk[,1] B<-mhk[,2] nYt=(Yt-mean(Yt))/sd1(Yt) reg(nYt,cbind (A,B))
Dostaneme nasledovný výstup:
Linear regresion
--------------------------------------
Estimated values of Y:
-1.48031 -1.358108 -0.8064217 -1.154319 -0.5668711 -0.3385706 -0.2570431 0.0690665 0.2592971 0.05556761 0.5719079 0.6534353 1.482505 0.8844593 1.985406
--------------------------------------
Summary from lm function:
Call:
lm(formula = Yt ~ m)
Residuals:
Min 1Q Median 3Q Max
-0.30647 -0.14758 -0.07144 0.15586 0.52841
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1.951e-15 6.361e-02 0.000 1.0000
mA -6.963e-01 4.599e-02 -15.139 3.5e-09 ***
mB -5.259e-01 2.154e-01 -2.442 0.0311 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.2464 on 12 degrees of freedom
Multiple R-squared: 0.9514, Adjusted R-squared: 0.9434
F-statistic: 117.6 on 2 and 12 DF, p-value: 1.311e-08
Zistili sme, že po odstránení multikolinearity má model menšiu chybu (Residual standard error). Pôvodná chyba bola 1.35 a teraz je už len 0.2464. Tento fakt si môžeme všimnúť aj na grafe. Preto upravený model je viac vhodný na modelovanie či prognózovanie ako pôvodný.
Nový model má rovnicu:
nYt= -1.951e-15- 6.963e-01*A- 5.259e-01*B + ut