Lineárna regresia

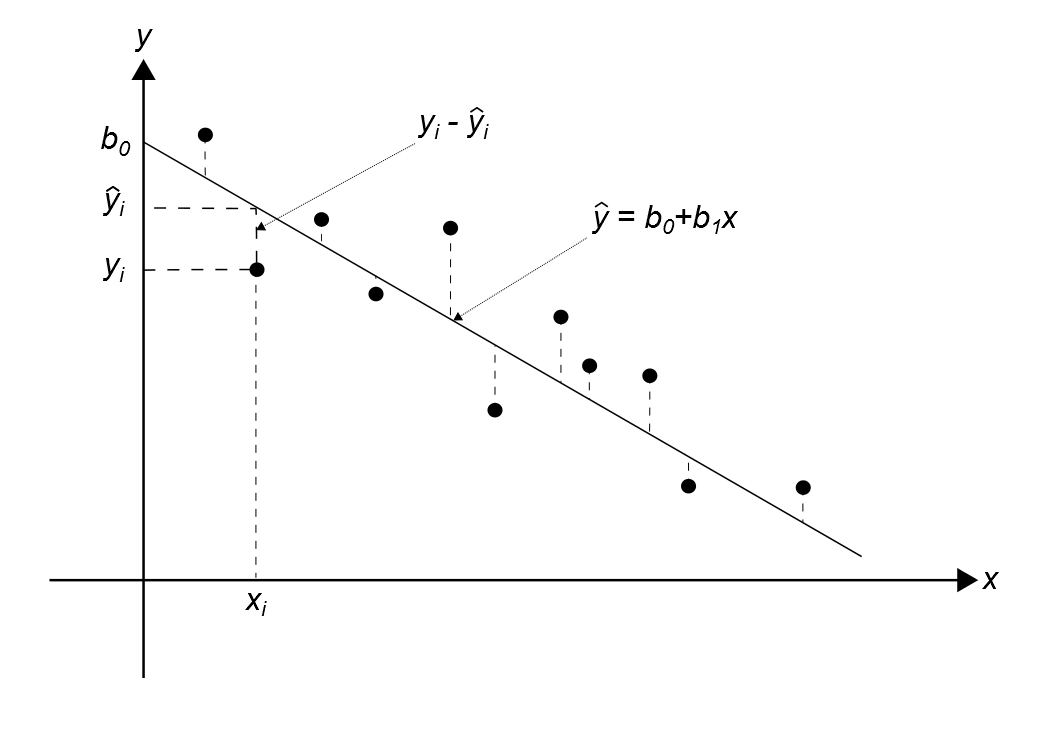
predstavuje aproximáciu daných hodnôt pomocou polynómu prvého rádu metódou najmenších štvorcov, inak povedané: hľadá sa priamka v grafe, aby súčet druhých mocnín (štvorcov) odchýlok (y_i - y^_i) jednotlivých bodov od priamky bol minimálny
môže všeobecne znamenať aj aproximáciu daných hodnôt [xi,yi] takou funkciou y_t = f(x, b₁ , …, b_k), ktorá sa dá vyjadriť lineárnou kombináciou y = b₁f₁(x)+ … + b_kf_k(x). Koeficienty b₁, …, b_k sú vypočítané metódou najmenších štvorcov. Platí kritérium (S):

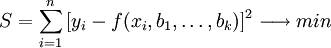
Majme jednorovnicový model:
yt = b₀ + b₁x_t1 + … + b_kx_tk + u_t ,pre t = 1, 2. …, n

Jednorovnicový model môžeme jednoduchšie zapísať v maticovom tvare ako:

y = Xb + u.

Potom odhad vektora parametrov označme ako b^ a vypočítané (teoretické) hodnoty vysvetľovanej premennej ako y^, pričom: y^ = Xb^ a skutočné hodnoty vysvetľovanej premennej ako y = Xb^ + e, kde e je vektor konkrétnych reziduálnych odchýlok, vypočítaných zo vzťahu:

e = y – Xb^ = y – y^

Odvodenie vzorca pre výpočet lineárnej regresie:

Pretože e je vektor, upravme túto požiadavku tak, aby súčet štvorcov jednotlivých odchýlok (zložiek vektora e) bol minimálny. Jedná sa teda o minimalizáciu skalárneho súčinu, ktorý môžeme napísať pomocou transpozície:

e^T e → min

Súčin bude minimálny, ak jeho deriváciu podľa b položíme rovnú nule:

(e^T e)' = [ (y - Xb^)^T (y – Xb^)]' = 0

Po použití pravidiel transpozície súčinu:

[y^T y - y^T Xb^ - b^^T X^T b^ - b^^T X^T y + b^^T X^T Xb^]' = 0

Po použití pravidiel pre deriváciu súčinu matíc:

2X^T y - 2X^T Xb^ = 0

Jednoduchou úpravou dostaneme:

b^ = (X^T X)^-1 X^T y

Výpočet

Vzorový príklad s metódami na odhad parametrov lineárnej regresie sa nachádza v tomto scripte.

Na odhad parametrov lineárnej regresnej funkcie (jednoduchá metóda najmenších štvorcov) môžme použiť viacero metód:

1. Výpočet vektora parametrov b cez matice Ukázať

1. Výpočet vektora parametrov b cez matice	Ukázať
Postup: 1. Načítanie vstupných vektorov 2. Postupné počítanie podľa vzorca 3. Vypísanie výsledku 1. Načítanie vstupných vektorov Dáta použité v tomto príklade nájdete tu: Odkazy na použité a reálne dáta 2. Postupné počítanie podľa vzorca: `Vytvoríme si pomocný vektor, ktorý bude tvoriť prvý stĺpec matice X (pozostávajúci z jednotiek), pomocou funkcie replicate(x=1,times=9).` pom = rep(1,9) `Následne potrebujeme vytvoriť samotnú maticu X načítaním hodnôt.` X<-matrix(c(pom,Pt,It),9,3) `Program vyžaduje zadanie rozmerov matice, na čo slúži funkcia array(vektory_matice,rozmery_matice).` X = array( c(pom,Pt,It) , c(9,3) ) `Kvôli kontrole si teraz vypíšeme maticu X.` X . [,1] [,2] [,3] [1,] 1 103 110 [2,] 1 102 114 [3,] 1 100 130 [4,] 1 94 135 [5,] 1 98 141 [6,] 1 97 152 [7,] 1 98 160 [8,] 1 97 165 [9,] 1 96 170 `Pre ďalší výpočet potrebujeme maticu X transponovať.` Xtran = t(X) `Z transponovanej matice vytvoríme maticu inverznú X'(uložená v premennej XXinv). Funkcia solve(matica) vytvorí inverznú maticu, kde násobenie matíc sa v R vykonáva pomocou %%.` XXinv = solve(Xtran %% X) `Na záver nasleduje výpočet parametrov lineárnej regresie, ktorý vložíme do premennej b.` b = XXinv %% Xtran %% Yt `3. Vypísanie výsledku` b `Výstup z programu R po vykonaní predchádzajúcich 3 krokov:` [1,] 10.43922788 [2,] -0.13838383 [3,] 0.09476636 `koeficienty regresnej funkcie:` 10.43923 … b0 – lokujúca konštanta/ aditívny člen/ absolútny člen -0.13838 … b1 0.09477 … b2

Postup:

1. Načítanie vstupných vektorov

2. Postupné počítanie podľa vzorca

3. Vypísanie výsledku

1. Načítanie vstupných vektorov

Dáta použité v tomto príklade nájdete tu: Odkazy na použité a reálne dáta

2. Postupné počítanie podľa vzorca:

Vytvoríme si pomocný vektor, ktorý bude tvoriť prvý stĺpec matice X (pozostávajúci z jednotiek), pomocou funkcie replicate(x=1,times=9).

pom = rep(1,9)

Následne potrebujeme vytvoriť samotnú maticu X načítaním hodnôt.

X<-matrix(c(pom,Pt,It),9,3)

Program vyžaduje zadanie rozmerov matice, na čo slúži funkcia array(vektory_matice,rozmery_matice).

X = array( c(pom,Pt,It) , c(9,3) )

Kvôli kontrole si teraz vypíšeme maticu X.

. [,1] [,2] [,3]
[1,] 1 103 110
[2,] 1 102 114
[3,] 1 100 130
[4,] 1 94 135
[5,] 1 98 141
[6,] 1 97 152
[7,] 1 98 160
[8,] 1 97 165
[9,] 1 96 170

Pre ďalší výpočet potrebujeme maticu X transponovať.

Xtran = t(X)

Z transponovanej matice vytvoríme maticu inverznú X'(uložená v premennej XXinv). Funkcia solve(matica) vytvorí inverznú maticu, kde násobenie matíc sa v R vykonáva pomocou %*%.

XXinv = solve(Xtran %*% X)

Na záver nasleduje výpočet parametrov lineárnej regresie, ktorý vložíme do premennej b.

b = XXinv %*% Xtran %*% Yt

3. Vypísanie výsledku

Výstup z programu R po vykonaní predchádzajúcich 3 krokov:

[1,] 10.43922788
[2,] -0.13838383
[3,] 0.09476636

koeficienty regresnej funkcie:

10.43923 … b0 – lokujúca konštanta/ aditívny člen/ absolútny člen
-0.13838 … b1
0.09477 … b2

2. Výpočet vektora parametrov b pomocou funkcie lm() Ukázať

2. Výpočet vektora parametrov b pomocou funkcie lm()	Ukázať
Postup: 1. Načítanie vstupných vektorov 2. Zavolanie funkcie lm() 3. Vypísanie výsledku 1. Načítanie vstupných vektorov Najprv si načítame dáta závislej premennej. Yt = scan() 6.1 7.3 9.6 10.2 10.1 11.3 12.2 12.5 13.2 `Teraz načítame nezávislé premenné.` Pt = scan() 103 102 100 94 98 97 98 97 96 It = scan() 110 114 130 135 141 152 160 165 170 2. Zavolanie funkcie lm(): `Celý krok pozostáva zo spustenia funkcie lm(), čo je funkcia na výpočet lineárneho modelu. Táto funkcia obsahuje podfunkciu cbind(), čo je funkcia, ktorá spája stĺpce do matice. Výstup funkcie vo forme lm(zav_velicina ~ vektor(matica_nezav_veliciny/velicin)) uložíme do premennej regresia.` regresia = lm(Yt ~ cbind(Pt,It)) 3. Vypísanie výsledku `Pre kontrolu si môžeme vypísať vektor parametrov modelu.` regresia Call: lm(formula = Yt ~ cbind(Pt, It)) Coefficients: (Intercept) cbind(Pt, It)Pt cbind(Pt, It)It 10.43923 -0.13838 0.09477 `Pre výpis podrobnejšieho výsledku funkcie lm() použijeme funkciu summary.` summary(regresia) Call: lm(formula = Yt ~ cbind(Pt, It)) Residuals: Min 1Q Median 3Q Max -0.50999 -0.13967 -0.06466 0.15977 0.67953 Coefficients: . Estimate Std. Error t value Pr(>\|t\|) (Intercept) 10.439228 7.450424 1.401 0.2107 cbind(Pt, It)Pt -0.138384 0.066137 -2.092 0.0813 . cbind(Pt, It)It 0.094766 0.008787 10.785 3.76e-05 * — Signif. codes: 0 ‘’ 0.001 ‘’ 0.01 ‘’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 0.374 on 6 degrees of freedom Multiple R-squared: 0.9814, Adjusted R-squared: 0.9752 F-statistic: 158 on 2 and 6 DF, p-value: 6.47e-06 koeficienty regresnej funkcie: 10.43923 … b0 – lokujúca konštanta/ aditívny člen/ absolútny člen -0.13838 … b1 0.09477 … b2 Estimate – odhad parametrov Std. Error – odhad štandardných odchýlok parametrov modelu t value – hodnota t štatistiky

Postup:

1. Načítanie vstupných vektorov

2. Zavolanie funkcie lm()

3. Vypísanie výsledku

1. Načítanie vstupných vektorov

Najprv si načítame dáta závislej premennej.

 Yt = scan()
6.1 7.3 9.6 10.2 10.1 11.3 12.2 12.5 13.2

Teraz načítame nezávislé premenné.

  Pt = scan()
103 102 100 94 98 97 98 97 96

 It = scan()
110 114 130 135 141 152 160 165 170

2. Zavolanie funkcie lm():

Celý krok pozostáva zo spustenia funkcie lm(), čo je funkcia na výpočet lineárneho modelu. Táto funkcia obsahuje podfunkciu cbind(), čo je funkcia, ktorá spája stĺpce do matice. Výstup funkcie vo forme lm(zav_velicina ~ vektor(matica_nezav_veliciny/velicin)) uložíme do premennej regresia.

 regresia = lm(Yt ~ cbind(Pt,It))

3. Vypísanie výsledku

Pre kontrolu si môžeme vypísať vektor parametrov modelu.

 regresia

Call:
lm(formula = Yt ~ cbind(Pt, It))

Coefficients:
(Intercept) cbind(Pt, It)Pt cbind(Pt, It)It
10.43923 -0.13838 0.09477

Pre výpis podrobnejšieho výsledku funkcie lm() použijeme funkciu summary.

 summary(regresia)

Call:
lm(formula = Yt ~ cbind(Pt, It))

Residuals:
Min 1Q Median 3Q Max
-0.50999 -0.13967 -0.06466 0.15977 0.67953

Coefficients:
. Estimate Std. Error t value Pr(>|t|)
(Intercept) 10.439228 7.450424 1.401 0.2107
cbind(Pt, It)Pt -0.138384 0.066137 -2.092 0.0813 .
cbind(Pt, It)It 0.094766 0.008787 10.785 3.76e-05 ***
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.374 on 6 degrees of freedom
Multiple R-squared: 0.9814, Adjusted R-squared: 0.9752
F-statistic: 158 on 2 and 6 DF, p-value: 6.47e-06

koeficienty regresnej funkcie:

10.43923 … b0 – lokujúca konštanta/ aditívny člen/ absolútny člen
-0.13838 … b1
0.09477 … b2

Estimate – odhad parametrov
Std. Error – odhad štandardných odchýlok parametrov modelu
t value – hodnota t štatistiky

3. Výpočet vektora parametrov b pomocou vlastnej funkcie	Ukázať
Táto funkcia vypočíta a vypíše odhadnuté hodnoty y, vykreslí graf hodnôt y a y^, a vypíše detailný výpis z funkcie lm (parametre, R2…) (Vlastnú funkciu nájdeme tu)

Zdroje:
Lineárni regrese tak nebo jinak[4.6.2015]
Metoda nejmensich ctvercu [4.6.2015]
Marček, D., Marček, M., Pančíková, L.: Ekonometria a soft computing. Žilina: EDIS, 2008 ISBN 978-80-8070-746-0

Lineárna regresia

Odvodenie vzorca pre výpočet lineárnej regresie:

Menu

Administrácia