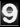Čoskoro bude text upravený.
Potrebné knižnice:
tseries (pre KPSS test)
Bude upravené.
Ide o modely, ktoré zachytávajú vplyv v predchádzajúcich hodnôt a hodnôt náhodných zložiek.
Príklad:
Dáta použité v tomto príklade nájdete tu: Odkazy na použité a reálne dáta
Identifikácia modelu
Prvým krokom k správnemu modelovaniu ekonomických procesov a následnému prognózovaniu je správna identifikácia modelu. Na identifikáciu slúžia autokorelačné a parciálne autokorelačné koeficienty a ich grafické znázornenie.
ACF a PACF koeficienty a korelogramy
V R-ku je ACF funkcia realizovaná nasledujúcim príkazom:
acf(x, lag.max = NULL,
type = c("correlation", "covariance", "partial"),
plot = TRUE, na.action = na.fail, demean = TRUE, ...)
Takže príkaz zadáme jednoducho:
acf1=acf(yt)
Na vypísanie jednotlivých koeficientov využijeme premennú acf1 do ktorej sme si výstup uložili.
acf1
Autocorrelations of series ‘yt’, by lag
0 1 2 3 4 5 6 7 8 9 10
1.000 0.494 -0.050 -0.265 -0.283 -0.072 0.219 0.196 -0.012 -0.093 -0.106
11 12 13 14 15 16 17 18 19 20
-0.075 0.031 0.014 -0.105 -0.124 -0.112 -0.091 0.003 0.157 0.182
Na vykreslenie korelogramu využijeme funkciu plot(), do ktorej ako parameter zadáme premennú acf1. Keďže je znázornený aj posun 0, ktorý však pre nás nemá žiadny význam, môžeme si funkciu trošku poupraviť aby znázorňovala hodnoty až od pozície 1.
plot(acf1[1:100])
Podobne je riešená aj funkcia PACF.
pacf(x, lag.max, plot, na.action, ...)
Takže príkaz urobíme obdobne:
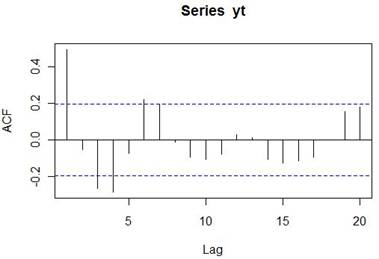
pacf1=pacf(yt)
Následne vypíšeme parciálne koeficienty a hneď aj korelogram.
pacf1
Partial autocorrelations of series ‘yt’, by lag
1 2 3 4 5 6 7 8 9 10 11
0.494 -0.388 -0.060 -0.149 0.133 0.163 -0.127 -0.062 0.065 -0.018 -0.034
12 13 14 15 16 17 18 19 20
-0.004 -0.104 -0.072 -0.022 -0.100 -0.052 -0.005 0.164 0.053
plot(pacf1[1:100])
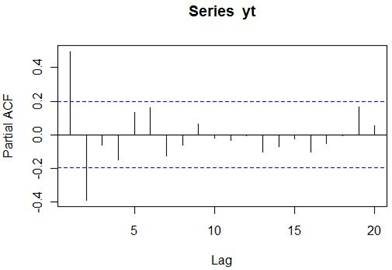
Podľa tabuľky priebehov ACF a PACF, ktorá je uvádzaná … môžeme identifikovať model.
Tento model je AR(2)
Identifikácia modelu na základe ACF a PACF nemusí byť vždy jednoznačná. V prípade nerozhodnosti môžeme využiť jedno z informačných kritérií, napríklad tzv. AIC kritérium. Vo všeobecnosti platí, že čím nižšia hodnota AIC, tým je model lepší v porovnaní s modelom s vyššou hodnotou AIC. V R je hodnota AIC definovaná ako záporné číslo. AIC je automaticky počítaná pri odhade samotných parametrov, tak jej hodnoty budú zobrazené neskôr.
Určenie stacionarity časového radu
Veľmi dôležitou podmienkou modelu je stacionarita časového radu. Stacionarita je nevyhnutná podmienka pre modelovanie časových radov prostredníctvom ARMA modelov. Zisťuje sa pomocou viacerých faktorov:
Bude upravené.
- Analýzou ACF funkcie
- Testami na integrovanosť dát (KPSS test). Je potrebné uviesť, že KPSS test má hypotézy postavené naopak ako ostatné testy. Pre nás je však dôležité že ak hodnota p-value je väčšia ako hladina významnosti tak je potvrdená stacionarita radu.
kpss.test(yt)
KPSS Test for Level Stationarity
data: yt
KPSS Level = 0.1062, Truncation lag parameter = 2, p-value = 0.1
Warning message:
In kpss.test(yt) : p-value greater than printed p-value
Ako nám R-ko aj napísalo, p-value je väčšia ako hladina významnosti, čiže rad je stacionárny.
Ak rad nie je stacionárny, existuje viacero možností, ako tento rad upraviť.
- odstránenie trendu
detrend(yt)
- logaritmovanie dát
log(yt)
- diferencovanie dát
diff(yt)
- kombináciou
Odhad parametrov modelu
Po identifikácii modelu a jeho prípadnej stacionarizácii možno prejsť k odhadu parametrov. Základný príkaz na zistenie parametrov modelu je nasledovný:
arima(x, order = c(0, 0, 0),
seasonal = list(order = c(0, 0, 0), period = NA),
xreg = NULL, include.mean = TRUE,
transform.pars = TRUE,
fixed = NULL, init = NULL,
method = c("CSS-ML", "ML", "CSS"),
n.cond, optim.method = "BFGS",
optim.control = list(), kappa = 1e6)
Ako môžeme vidieť, príkaz obsahuje mnoho parametrov, ale pre nás budú najdôležitejšie tieto:
x – premenná, ktorá obsahuje dáta časového radu,
order – stupeň modelu. Parametre c(p,d,q), kde p je stupeň AR, d stupeň diferencie a q stupeň MA modelu. V našom prípade bude order vyzerať nasledovne: order=c(2,0,0).
Samotné spustenie príkazu arima:
ar2=arima(yt,order=c(2,0,0))
ar2
arima(x = yt, order = c(2, 0, 0))
Coefficients:
ar1 ar2 intercept
0.7108 -0.4249 28.6500
s.e. 0.0923 0.0936 0.4559
sigma^2 estimated as 10.55: log likelihood = -260.02, aic = 528.04
Pre ďalšie výpočty bude potrebovať samotné parametre výstupu. Tie získame pomocou funkcie coef(). Voláme ho tak, že napíšeme názov premennej, kde je uložený arima model, potom napíšeme znak $ a nakoniec coef.
ar2$coef
ar1 ar2 intercept
0.7108021 -0.4248993 28.6500239
Vyššie sme si spomínali, že jedno z kritérií pre identifikáciu modelu je AIC kritérium. Ak sme si všimli, vo výstupe sa objavila hodnota aic=528,04. Môžeme teda skúsiť pre kontrolu zadať iný model, či bude hodnota aic menšia.
ar3=arima(yt,order=c(2,0,1))
Coefficients:
ar1 ar2 ma1 intercept
0.8676 -0.4997 -0.1922 28.6525
s.e. 0.2067 0.1187 0.2388 0.4161
sigma^2 estimated as 10.49: log likelihood = -259.79, aic = 529.57
Ako môžeme vidieť, pri zadaní iného modelu je hodnota aic väčšia, takže z toho vyplýva že pôvodné definovanie modelu bolo správne(lepšie).
Kontrola reziduí modelu
Kontrola reziduí identifikovaného a odhadnutého modelu budeme realizovať pomocou metódy Arch test. Jeho úlohou je zistiť, či sa v reziduách nachádza podmienená heteroskedasticita. Tento test sa nachádza v balíku FinTS, takže je potrebné si tento balík stiahnuť a nainštalovať.
Test je v R-ku definovaný nasledovne:
ArchTest (x, lags=12, demean = FALSE)
kde x je rad reziduí, lags je počet posunov(odporúča sa hodnoty 1, 5, 12), parameter demean nás zatiaľ zaujímať nemusí.
Reziduá získame pomocou funkcie arima. Okrem komponentu $coef obsahuje arima aj komponent $residuals, ktorý nám vráti reziduá modelu. Takže volanie funkcie ArchTest bude vyzerať takto:
ArchTest(ar2$residuals,lags=1)
ARCH LM-test; Null hypothesis: no ARCH effects
data: ar2$residuals
Chi-squared = 0.0573, df = 1, p-value = 0.8109
Kritériom vyhodnocovania je okrem chí kvadrát testu i hodnota p-value, ktorou sa budeme riadiť i my. Vo všeobecnosti možno povedať, že ak je hodnota p-value väčšia ako hladina významnosti, rezíduá tvoria biely šum, neexistuje tam podmienená heteroskedasticita a teda rezíduá sú v poriadku.
Predikcia časového radu
Prognózovanie sa realizuje pomocou funkcie predict(). Parametre funkcie sú odhadovaný model, v našom prípade ar2 a počet požadovaných prognóz. Takže v našom prípade bude príkaz vyzerať nasledovne:
prog=predict(ar2,9)
$pred #prognózované rady
Time Series:
Start = 101
End = 109
Frequency = 1
[1] 32.15551 29.53138 27.78701 27.66211 28.31450 28.83130 28.92144 28.76592 28.61708
$se #štandardná odchýlka
Time Series:
Start = 101
End = 109
Frequency = 1
[1] 3.247405 3.984184 3.992717 4.071160 4.126931 4.129397 4.133579 4.138070 4.138477
Prognózované časové rady si môžeme vykresliť do pôvodného grafu. K prognózovaným hodnotám pristupujeme pomocou známeho znaku $ a prípony pred. Postup je nasledovný:
Vykreslíme graf s pôvodným modelom, ale os x rozšírime na 110.
plot(yt,type="b", xlim=c(0,110))
A následne pomocou funkcie lines() pridáme do grafu prognózované hodnoty:
lines(prog$pred, type="b", col="red")
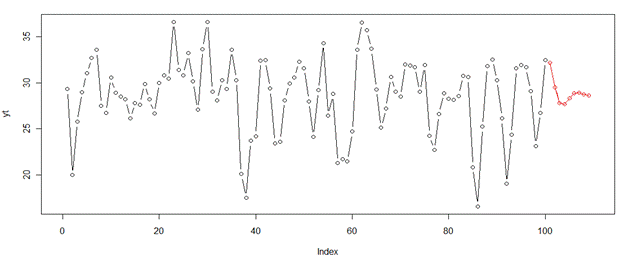
Z výpisu premennej prog sú známe nasledovné predikované hodnoty:
32.15551
29.53138
27.78701
27.66211
28.31450
28.83130
28.92144
28.76592
28.61708