Kalmanova filtrácia

Kalmanova filtrácia je metóda, ktorá slúži na získanie aktuálneho, ale aj budúceho stavu dynamického systému. Jej hlavným nástrojom je Kalmanov filter, ktorým je možné odhadnúť premenné zo širokej škály procesov. Najčastejšie je využívaný v technológii ako GPS, vývoji vojenskej techniky a pre riadenie zložitých dynamických systémov. Svoje zastúpenie má však aj v počítačovej technike a ekonomických vedách, napríklad v podobe analýzy časových radov, ktoré možno vyjadriť v tzv. lineárnej stavovej forme.

Aby bolo možné použiť Kalmanov filter pre odstránenie šumu zo signálu, skúmaný proces pozorovania musí byť možné popísať lineárnym systémom. Tento systém je vyjadrený dvomi rovnicami, a to stavovou rovnicou a rovnicou pozorovaní. Stavová rovnica dynamického systému má tvar:

x_t = Ax_t-1 + Bu_t-1 + w_t-1

xt – stavový vektor, predstavujúci minimálnu hodnotu údajov, ktorou je možné popísať správanie sa dynamického systému,
A – prechodová matica, reprezentuje maticu prechodu stavového vektora, zo stavu v čase t-1 do času t,
B – postupnosť matíc parametrov exogénnych premenných,
ut – vektor špecifikovaných exogénnych premenných, ktoré ovplyvňujú xt,
wt – procesný šum, o ktorom sa predpokladá, že má nulovú strednú hodnotu a známu kovariančnú maticu Q.

Druhá rovnica, ktorou je lineárny dynamický systém reprezentovaný, je rovnica pozorovaní v tvare:

y_t = Hx_t + v_t

yt – pozorovanie v čase t,
H – matica pozorovaní,
vt – šum pozorovaní s nulovou strednou hodnotou a známou kovariančnou maticou R. Šumy vt a wt sú navzájom nezávislé.

Riešenie Kalmanovej filtrácie v R

Na riešenie Kalmanovej filtrácie v prostredí R môžme použiť funkciu StructTS()

StructTS(x, type = c("level", "trend", "BSM"), init = NULL, fixed = NULL, optim.control = NULL)

Popis premenných:
x – časový rad (povolené sú aj chýbajúce hodnoty),
type – typ modelu (napríklad BSM – základný štrukturálny model),
init – počiatočné hodnoty rozptylu parametrov,
fixed – nepovinný číselný vektor rovnakej dĺžky ako celkový počet parametrov.

Príklad na Kalmanovu filtráciu

V tomto príklade využijeme štvrťročné dáta získané z českého štatistického úradu, konrétne 1. dokument a 1. stĺpec dokumentu, 1. hárok, čo predstavuje údaje o ľuďoch, ktorí strávili viac ako 4 noci v hoteloch v ČR.

Načítame si dáta:
Dáta použité v tomto príklade nájdete tu: Odkazy na použité a reálne dáta

Z dát si prostredníctvom funkcie ts vytvoríme vektor s hodnôt časového radu so štvrťročnou periódou (ts_freq=4) a so začiatkom v roku 2003 (ts_start = 2003). Následne si dáta vykreslíme pomocou funkcie plot čiarkovanou čiarou (lty=”dotted”):

my_cv_data <- c(1446.10,1940.17,5576.95,978.36,1410.89,1500.21,5068.24,953.86,1338.31,
2036.41,5005.75,1052.94,1488.87,1938.82,5130.36,1347.81,1516.84,1922.73,
5792.79,1220.65,1431.42,1754.18,5648.29,1355.09)
ts_freq <- 4
ts_start <- 2003
mcdata_ts<-ts(my_cv_data,start=ts_start,frequency=ts_freq)
plot(mcdata_ts, lty="dotted")

Načítame si knižnicu forecast, ak ju nemáme, tak si ju nainštalujeme.
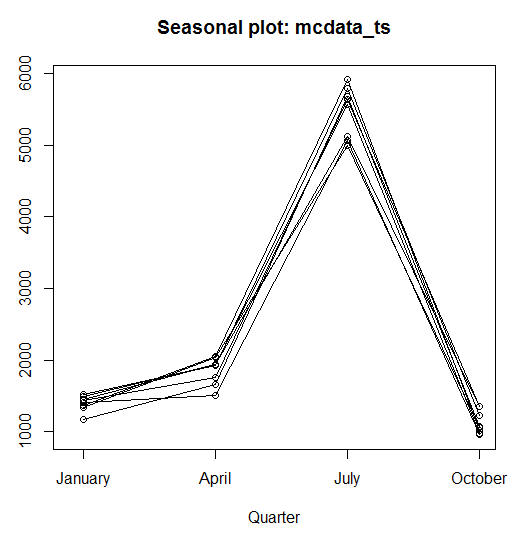
Následne zobrazíme sezónny graf našich dát časového radu:

library(forecast)
seasonplot(mcdata_ts)

Priradíme do vektora kts odhad Kalmanovým filtrom. Z vektora si kts si potom spravíme predikcie na 4 kvartály pomocou generickej funkcie predict

kts<-StructTS(mcdata_ts,type="BSM")
prog_kts<-predict(kts,4)

Na vizualizáciu grafu potrebujeme nasledovnú funkciu. Funkcia vykreslí reálne dáta čiarkovanou čiarou, dáta odhadnuté kalmanom modrou a predikcie červenou čiarou. Ako parametre potrebuje dáta data_ts, objekt kalmanovho filtra kts,  prognózu prog_kts, vektor so začiatkom časového radu t.start a vektor s frekvenciou t.freq.

plot_kalman <- function(data_ts, kts, prog_kts, t.start, t.freq) {
  prog_kts <- prog_kts$pred
  kts_s <- kts$fitted[,1]+kts$fitted[,2]+kts$fitted[,3]
  min_v <- min(data_ts, prog_kts, kts_s)
  max_v <- max(data_ts, prog_kts, kts_s)
  kts_w_prog<-ts(c(kts_s, prog_kts), start=t.start, freq=ts_freq)
  plot(data_ts,xlim=attr(kts_w_prog,"tsp")[1:2],
       ylim = c(min_v,max_v), lty="dotted")
  lines(kts_w_prog,col="red")
  lines(kts_s,col="blue")
}

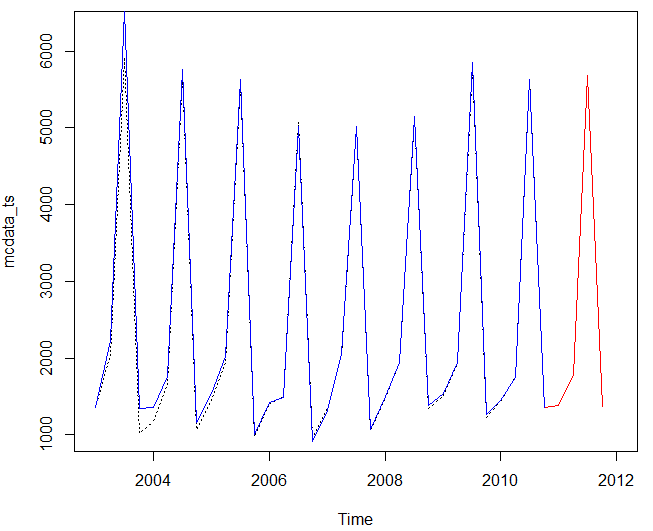
Funkcii priradíme naše parametre a vykreslí nám graf

plot_kalman(mcdata_ts, kts, prog_kts, ts_start, ts_freq)

Odmocnenú priemernú štvorcovú chybu (RMSE) môžeme získať tak, že zosumujeme rozdiel modelu odhadnutého kalmanom kts$fitted a prvotných dát my_cv_data. Tieto rozdiely umocníme na druhú, sčítame, podelíme počtom pozorovaní a následne odmocníme

RMSE_kalman <- sqrt(sum((rowSums(kts$fitted) - mcdata_ts)^2)/length(mcdata_ts))

[1] 136.4347


Zdroje:
Považanec, P.:DIPLOMOVÁ PRÁCA:Optimalizácia softvérového riešenia prognózovania časových radov ekonomických dát. 2010