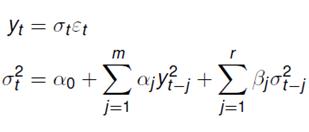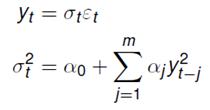Potrebné knižnice:
library(fGarch)
library(tseries)
library(FinTS)
GARCH modely sú navrhnuté tak, aby zachytili určité charakteristiky spoločné pre finančné časové rady: tučné konce, zhlukovanie rozptylu, pretrvávanie, priťahovanie sa k dlhodobej úrovni, efekt zo zadĺženia alebo pákový efekt.
ARCH modely sú postavené na predpoklade heteroskedasticity tj., že rozptyl (štandardná odchýlka) náhodnej zložky modelu sa v čase mení, alebo inak povedané rozptyl hodnôt časového radu je určovaný predchádzajúcimi hodnotami časového radu.
Modelovanie (G)ARCH v jazyku R prebieha takmer rovnako ako modelovanie ARIMA procesov. Najprv je potrebné určiť typ a stupeň G(ARCH) procesu, nasleduje odhad parametrov modelu a diagnostika.
Určenie stupňa (G)ARCH modelu
Mnohými aplikáciami týchto modelov bolo zistené, že veľkú väčšinu existujúcich reálnych procesov je možné modelovať za pomoci procesu GARCH(1,1). Preto i my budeme zväčša využívať GARCH modely 1.stupňa ako prvotný (častokrát i jediný) stupeň (G)ARCH k modelovaniu procesov.
Odhad parametrov (G)ARCH modelu
Základný príkaz na modelovanie (G)ARCH efektov v jazyku R je garchFit(). Parametre, ktor0 do nej vstupuj[ sú: arma(1,2,1), garch(1,1) a dáta. Výpočet typu a stupňa AR(i)MA je v druhej sekcií a do modelu ho dávame, lebo chceme robiť prognózy celého procesu a nie len jeho reziduí.
Príklad:
Nasleduje načítanie dát:
Dáta použité v tomto príklade nájdete tu: Odkazy na použité a reálne dáta
Ďalej už iba zavolať samotnú funkciu garchFit()
model = garchFit(~arma(8,1,8)+garch(1,1), data = data)
Výsledok (ukázana iba časť výpisu)
Series Initialization:
ARMA Model: arma
Formula Mean: ~ arma(1, 2, 1)
GARCH Model: garch
Formula Variance: ~ garch(1, 1)
ARMA Order: 1 0
Max ARMA Order: 1
GARCH Order: 1 1
Max GARCH Order: 1
Maximum Order: 1
Conditional Dist: norm
h.start: 2
llh.start: 1
Length of Series: 100
Recursion Init: mci
Series Scale: 4.132703
Ak chceme podrobnejší výpis dáme:
summary (model)
Diagnostika rezíduí (G)ARCH modelu
Odhadnutý model je ešte potrebné verifikovať. Na to nám poslúžia rezíduá modelu, ktoré musia byť štadardizované a to dosiahneme príkazom:
GarchRezidua = model@residuals/model@sigma.t
Samotné rezíduá je možné verifikovať pomocou archTestu, Ljung-box štatistiky, BDS testu, grafická diagnostika pomocou teoretických kvantilov.
ArchTest
ArchTest nájdete popísaný v sekcií arima modlely. Zmena je v tom že v našom prípade vkladáme rezíduá z Garch procesu. Testujeme nulovú hypotézu, či sa v rezíduách nachádza ďalší ARCH efekt. Ak hodnota p-value je vačšia ako hladina významnosti, príjmame túto hypotézu. Parametre Lags sa odporúča nastaviť na parametre(1,5,12).
ArchTest(GarchRezidua, lags =1)
Výsledok
ARCH LM-test; Null hypothesis: no ARCH effects
data: GarchRezidua
Chi-squared = 0.0582, df = 1, p-value = 0.8094
Diagnostika pomocou Ljung-box štatistiky
Vo výstupe summary(model) z predchádzajúcej časti sa nachádza Ljung-box štatistika. Tu si taktiež všímame hodnotu p-value, ktorá ak je menšia než hladina významnosti, rezíduá sú významné.
Standardised Residuals Tests:
Statistic p-Value
Jarque-Bera Test R Chi^2 6.316023 0.04251018
Shapiro-Wilk Test R W 0.9645913 0.00866055
Ljung-Box Test R Q(10) 37.45633 4.717499e-05
Ljung-Box Test R Q(15) 41.64911 0.0002544548
Ljung-Box Test R Q(20) 47.70409 0.0004679968
Ljung-Box Test R^2 Q(10) 6.301758 0.7893057
Ljung-Box Test R^2 Q(15) 10.42755 0.7920196
Ljung-Box Test R^2 Q(20) 11.74053 0.9247172
LM Arch Test R TR^2 10.19812 0.5985843
Diagnostika rezíduí pomocou BDS testu
Tvar BDS testu je nasledovný bds.test. Tu sa opäť riadime hodnotou p-value, ktorá ak je väčšia ako hladina významnosti, tak model je v poriadku a test nepotvrdil výskyt GARCH efektu v rezíduách. V našom prípade to vyzerá:
bds.test(GarchRezidua)
Výsledok
BDS Test
data: GarchRezidua
Embedding dimension = 2 3
Epsilon for close points = 0.5025 1.0050 1.5075 2.0100
Standard Normal =
[ 0.5025 ] [ 1.005 ] [ 1.5075 ] [ 2.01 ]
[ 2 ] -0.6156 0.4706 0.4590 0.6581
[ 3 ] -0.2098 1.5286 1.3965 1.5571
p-value =
[ 0.5025 ] [ 1.005 ] [ 1.5075 ] [ 2.01 ]
[ 2 ] 0.5382 0.6379 0.6463 0.5105
[ 3 ] 0.8338 0.1264 0.1626 0.1194
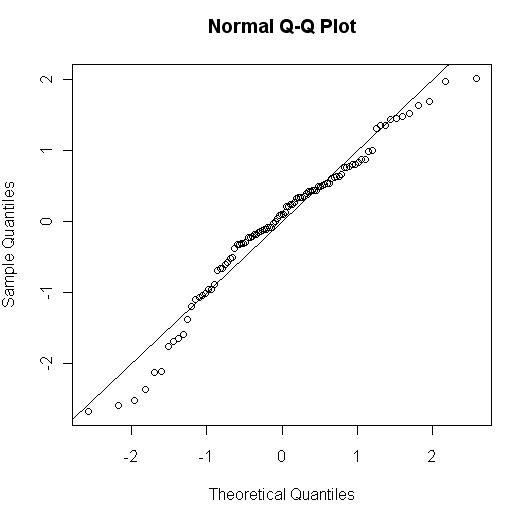
Grafická diagnostika pomocou teoretických kvantilov
Táto kontrola spočíva v grafickej kontrole medzi teoretickými kvantilmi normálneho rozdelenia a kvantilmi rozdelenia rezíduí. V R je to nasledovne:
qqnorm(GarchRezidua) abline(0,1)
Výsledný zápis (G)ARCH modelu
Pre zapísanie modelu pomocou rovnice sú potrebné koeficienty, ktoré sme dostali pri podrobnejšom výpise modelu, pre model GARCH sú najdôležitejšie koeficienty alpha a beta:
Error Analysis:
Estimate Std. Error t value Pr(>|t|)
mu 15.55206 3.28790 4.730 2.24e-06 ***
ar1 0.55890 0.10055 5.558 2.73e-08 ***
ar2 -0.32223 0.11429 -2.819 0.004811 **
ar3 0.30710 0.10334 2.972 0.002961 **
ar4 -0.34862 0.11073 -3.148 0.001641 **
ar5 0.07799 0.08941 0.872 0.383078
ar6 0.38467 0.05494 7.002 2.53e-12 ***
ar7 -0.06946 0.04989 -1.392 0.163867
ar8 -0.12594 0.05246 -2.401 0.016372 *
omega 0.03447 0.01124 3.067 0.002164 **
alpha1 1.00000 0.25621 3.903 9.50e-05 ***
beta1 0.35933 0.09608 3.740 0.000184 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Výsledný zápis modelu (G)ARCH:
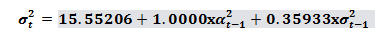
Zdroje:
Bábel, J.:DIPLOMOVÁ PRÁCA: Moderné prognostické metódy v modelovaní vysokofrekvenčných dát. 2008
Falát, L., Laštík, T., Tkáč P.: FRI MANUÁL v1.0